Yaleで、遊んで学ぶ日々。
Yaleで、遊んで学ぶ日々。
囲碁、ときどきプログラミング、ところにより経済。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
【前回】
【年齢調整死亡率, 標準化死亡比:人口構成を調整する】
粗死亡率の弱点は、人口構成が異なる場合の比較が難しいところにある。そこで考え出されたのが年齢調整死亡率 (direct age-adjusted mortality rate, DAR) だ。DARは次のように定義される。
DAR(i) = Σ_k [ d(i,k) / n(i,k) ] * R(k)
k: 年齢グループ
d(i,k): 地域iにおけるグループkの死亡数
n(i,k):地域iにおけるグループkの人口
R(k): 標準人口構成におけるグループkの割合
式は多少複雑だが、理屈はシンプルだ。まず、グループごとに死亡率を求める。DARは、「そのグループ別死亡率のもとで、仮に標準的な人口構成だったとした場合」の死亡率だ。だから、人口構成が標準人口構成と同一である場合(つまり n(i,k) / n(i) = R(k) )には、DARとCMRは一致する。
標準人口は何でも良い。厚生労働省では、今のところ昭和60年のモデル人口が用いられているようだ(→厚生労働省:年齢調整死亡率について)。
また、一般には年齢構成について調整されることが多いが、実際には人口をグルーピングする方法は何でも良い。性別や職業・産業構成などで調整するのも時に有用だろう。
下図では、千葉県の心疾患(高血圧性を除く)による死亡について、性・年齢5歳階級グループで調整した各市町村のDARを人口とプロットしている。標準人口には、同年の千葉県全体の人口構成を用いた。CMRに見られたような負の相関が消えている。間接的ではあるが、CMRと人口規模の負の相関が人口構成を介する擬似相関であることを示唆している。
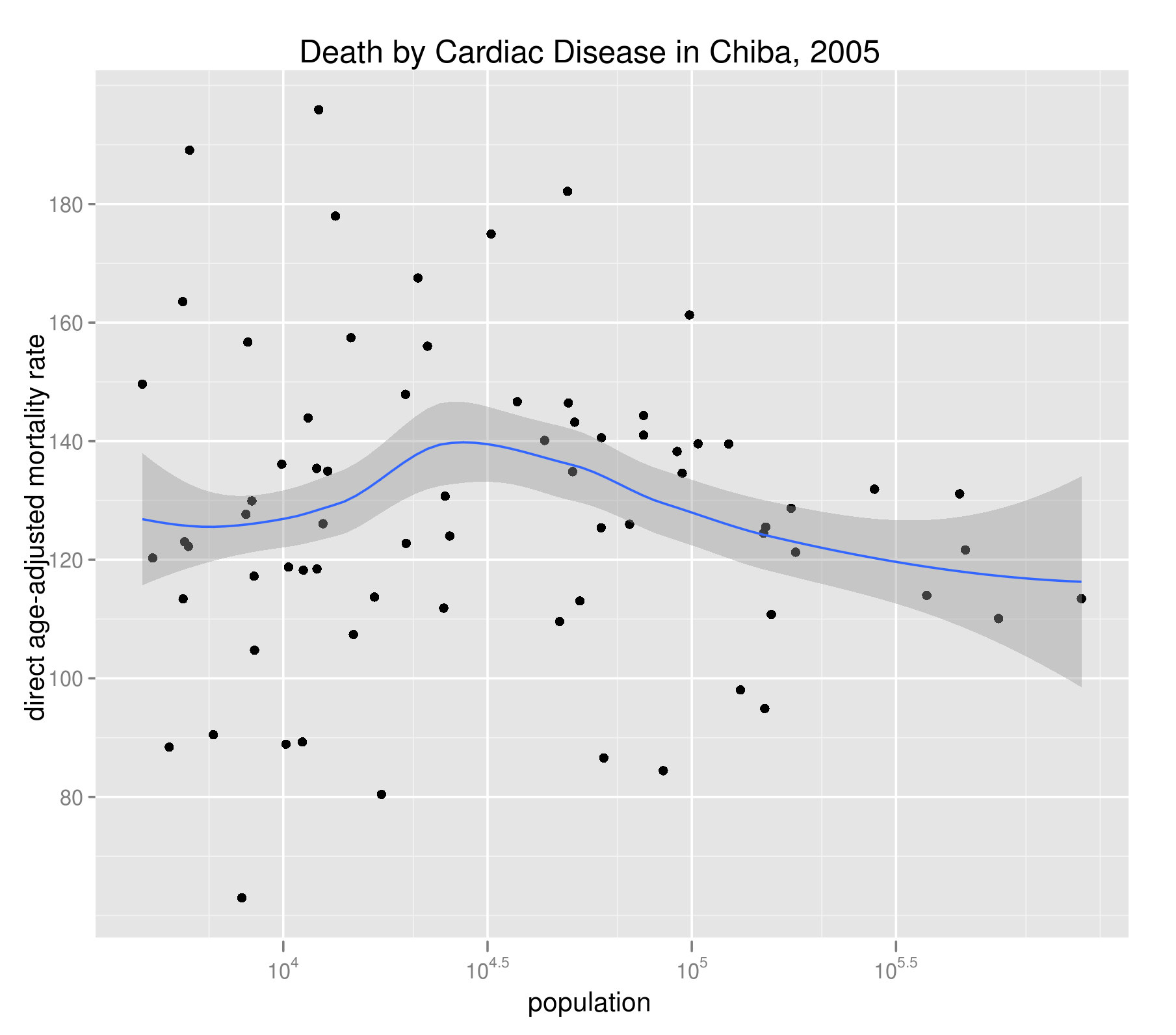
DARの1つの弱点は、詳細な死亡データが必要となる点である。グループ別の死亡者数(数式でのd(i,k))は、細かすぎて手に入らないことも多い。この点をカバーする代替指標の1つが、標準化死亡比(standardized mortality rate, SMR)だ。
SMR(i) = d(i) / Σ_k [ n(i,k) * P(k) ]
P(k): 標準的なグループkの死亡率
定義の分母は、標準的なグループkの死亡率と地域iの人口構成から計算される「予想死亡者数」となっており、SMRはその「予想死亡者数」が実際の死亡者数からどれだけ乖離しているかを表す指標だ。一般には、さらに100倍して100を基準とすることも多い。
SMRの1つの問題は、P(k)をどう定義するかだが、これには地域iの属する上位地域の死亡率を用いることが多い。例えば千葉県の市町村のSMRを計算する時には、千葉県全体の死亡率を用いるのが一案である。各都道府県のSMRの算出には日本全国の、各国のSMRの算出には世界全体の死亡率、といった具合だ。
下図には、千葉県内の各市町村の心疾患(高血圧性を除く)に関するSMRとその人口の散布図を示した。グループ分けは、同じく性・年齢5歳階級で行っている。DARとよく似ており、人口構成による擬似相関はきっちり排除できている。
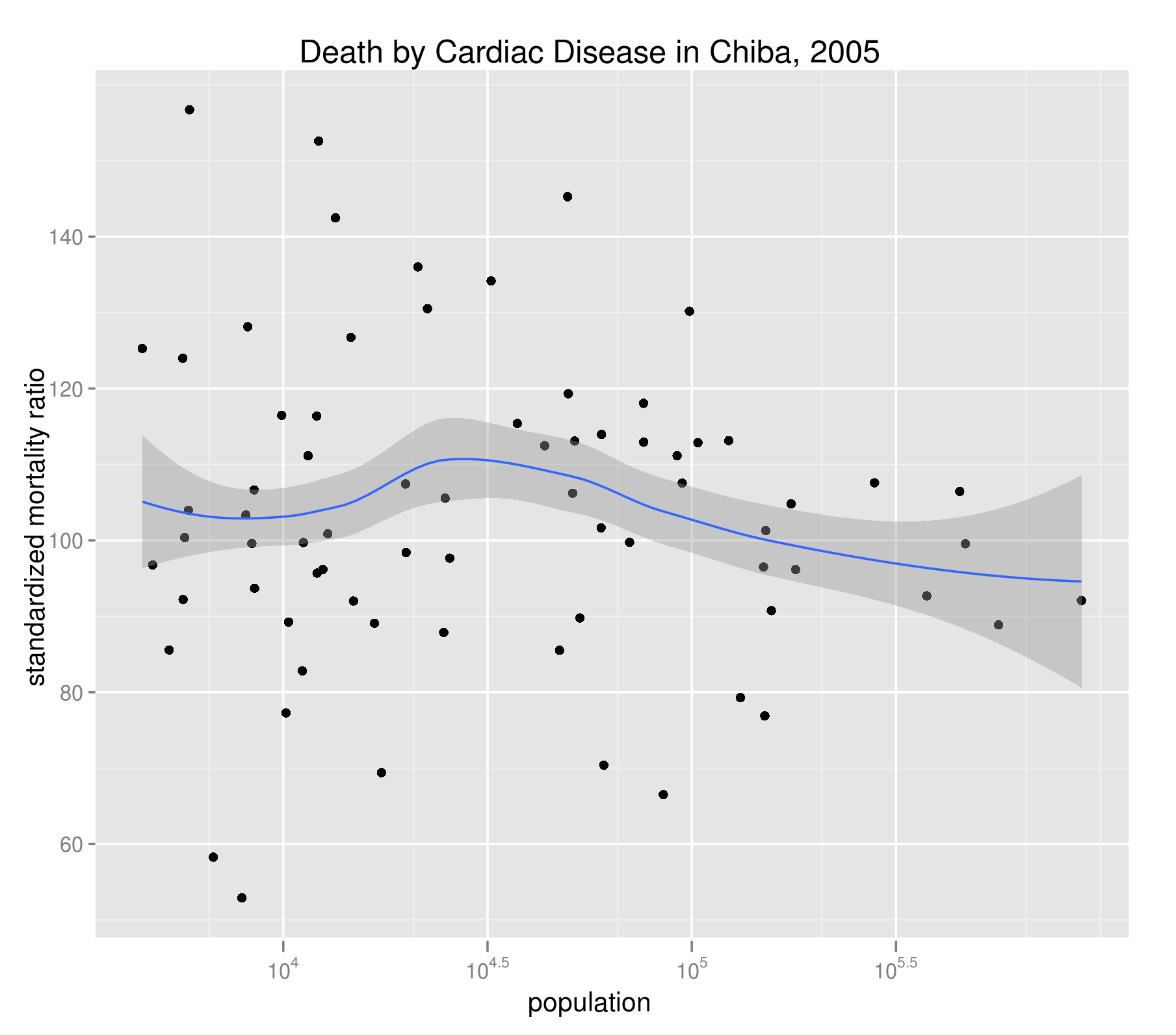
SMRの計算に必要な死亡データは地域別の総死亡数(d(i))だけなので、DARに比べてデータ面での要請は緩い。一方、その挙動はDARに近いのでなかなか優秀な指標のようだ。
下図では、粗死亡率 (CMR), 年齢調整死亡率 (DAR), 標準化死亡比 (SMR) の3指標の関係を散布図に表した。DARとSMFの線形相関が極めて強く、一方CMRは他の指標とそこそこの相関を持つにすぎないことが分かる。
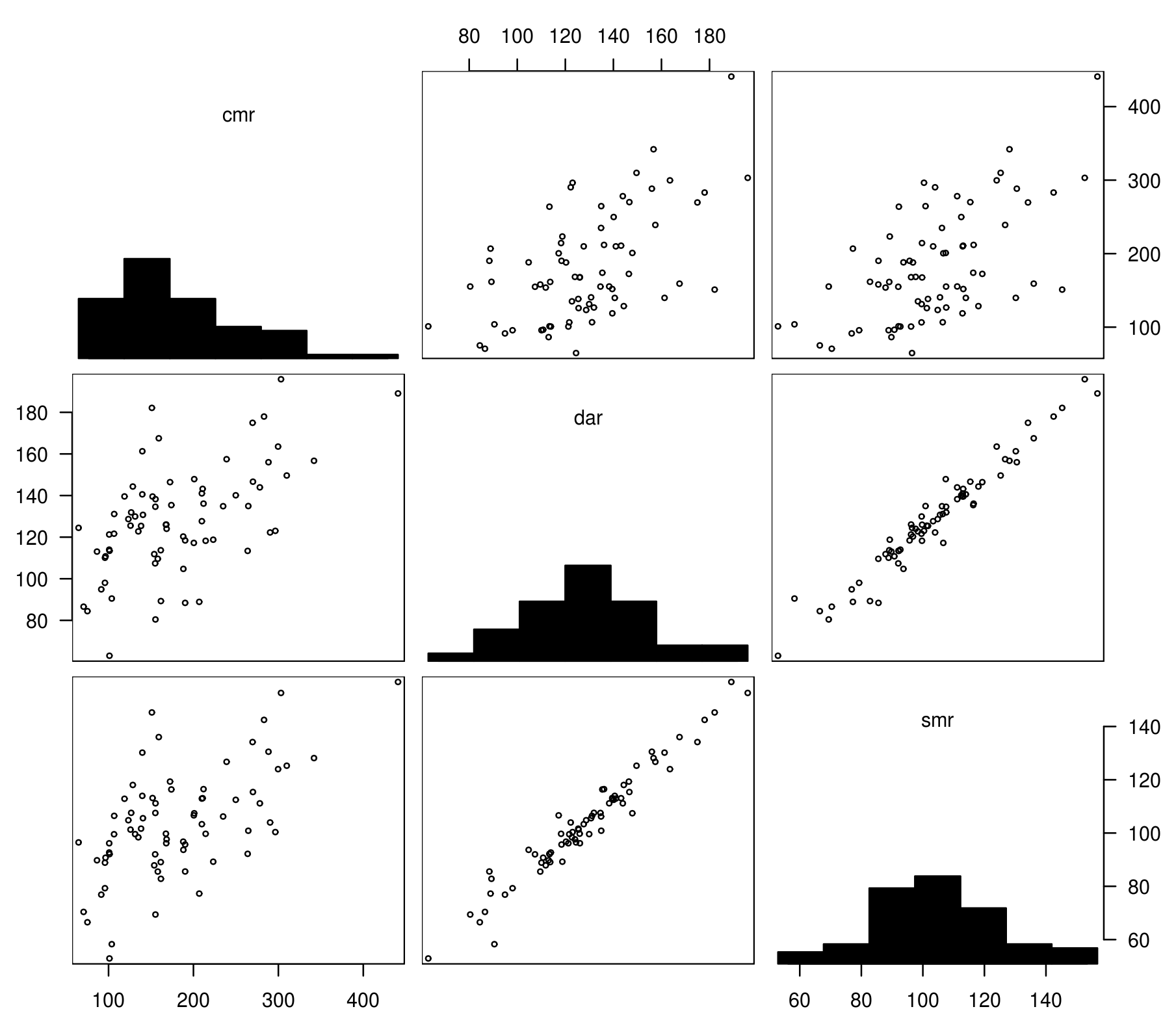
さて、死亡指標の比較には、年齢調整死亡率 (DAR) と 標準化死亡比 (SMR) の2つが非常によく用いられるが、それでも弱点がないわけではない。両指標の1つの弱点は、小地域における不安定性である。
先のグラフからも見て分かる通り、DARもSMRも、人口が小さくなるにつれて上下の振れ幅が大きくなっている(CMRも同様)。心疾患(高血圧性を除く)は比較的頻度の高い死因なので、一般には小規模地域における不安定性はもっと深刻になりうる。
端的に言えば、不安定性の原因はデータ不足にある。人口規模の小さい地域においては大数の法則が十分に成立しないため、死亡率が収束しきらないわけである。そこで、データ不足を補う方法を次に考える。
【つづき】
【年齢調整死亡率, 標準化死亡比:人口構成を調整する】
粗死亡率の弱点は、人口構成が異なる場合の比較が難しいところにある。そこで考え出されたのが年齢調整死亡率 (direct age-adjusted mortality rate, DAR) だ。DARは次のように定義される。
DAR(i) = Σ_k [ d(i,k) / n(i,k) ] * R(k)
k: 年齢グループ
d(i,k): 地域iにおけるグループkの死亡数
n(i,k):地域iにおけるグループkの人口
R(k): 標準人口構成におけるグループkの割合
式は多少複雑だが、理屈はシンプルだ。まず、グループごとに死亡率を求める。DARは、「そのグループ別死亡率のもとで、仮に標準的な人口構成だったとした場合」の死亡率だ。だから、人口構成が標準人口構成と同一である場合(つまり n(i,k) / n(i) = R(k) )には、DARとCMRは一致する。
標準人口は何でも良い。厚生労働省では、今のところ昭和60年のモデル人口が用いられているようだ(→厚生労働省:年齢調整死亡率について)。
また、一般には年齢構成について調整されることが多いが、実際には人口をグルーピングする方法は何でも良い。性別や職業・産業構成などで調整するのも時に有用だろう。
下図では、千葉県の心疾患(高血圧性を除く)による死亡について、性・年齢5歳階級グループで調整した各市町村のDARを人口とプロットしている。標準人口には、同年の千葉県全体の人口構成を用いた。CMRに見られたような負の相関が消えている。間接的ではあるが、CMRと人口規模の負の相関が人口構成を介する擬似相関であることを示唆している。
DARの1つの弱点は、詳細な死亡データが必要となる点である。グループ別の死亡者数(数式でのd(i,k))は、細かすぎて手に入らないことも多い。この点をカバーする代替指標の1つが、標準化死亡比(standardized mortality rate, SMR)だ。
SMR(i) = d(i) / Σ_k [ n(i,k) * P(k) ]
P(k): 標準的なグループkの死亡率
定義の分母は、標準的なグループkの死亡率と地域iの人口構成から計算される「予想死亡者数」となっており、SMRはその「予想死亡者数」が実際の死亡者数からどれだけ乖離しているかを表す指標だ。一般には、さらに100倍して100を基準とすることも多い。
SMRの1つの問題は、P(k)をどう定義するかだが、これには地域iの属する上位地域の死亡率を用いることが多い。例えば千葉県の市町村のSMRを計算する時には、千葉県全体の死亡率を用いるのが一案である。各都道府県のSMRの算出には日本全国の、各国のSMRの算出には世界全体の死亡率、といった具合だ。
下図には、千葉県内の各市町村の心疾患(高血圧性を除く)に関するSMRとその人口の散布図を示した。グループ分けは、同じく性・年齢5歳階級で行っている。DARとよく似ており、人口構成による擬似相関はきっちり排除できている。
SMRの計算に必要な死亡データは地域別の総死亡数(d(i))だけなので、DARに比べてデータ面での要請は緩い。一方、その挙動はDARに近いのでなかなか優秀な指標のようだ。
下図では、粗死亡率 (CMR), 年齢調整死亡率 (DAR), 標準化死亡比 (SMR) の3指標の関係を散布図に表した。DARとSMFの線形相関が極めて強く、一方CMRは他の指標とそこそこの相関を持つにすぎないことが分かる。
さて、死亡指標の比較には、年齢調整死亡率 (DAR) と 標準化死亡比 (SMR) の2つが非常によく用いられるが、それでも弱点がないわけではない。両指標の1つの弱点は、小地域における不安定性である。
先のグラフからも見て分かる通り、DARもSMRも、人口が小さくなるにつれて上下の振れ幅が大きくなっている(CMRも同様)。心疾患(高血圧性を除く)は比較的頻度の高い死因なので、一般には小規模地域における不安定性はもっと深刻になりうる。
端的に言えば、不安定性の原因はデータ不足にある。人口規模の小さい地域においては大数の法則が十分に成立しないため、死亡率が収束しきらないわけである。そこで、データ不足を補う方法を次に考える。
【つづき】
PR
| 死亡指標のいろは (1) << | HOME | >> 一目置かれる棋士 |
Calender
| 01 | 2026/02 | 03 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Search in This Blog
Latest Comments
[03/30 川内のばば山田]
[03/30 川内のばば山田]
[08/06 Aterarie]
[07/05 Agazoger]
[07/01 Thomaskina]
Latest Posts
(11/16)
(04/28)
(04/16)
(04/11)
(04/05)
Latest Trackbacks
Category
Access Analysis

