Yaleで、遊んで学ぶ日々。
Yaleで、遊んで学ぶ日々。
囲碁、ときどきプログラミング、ところにより経済。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
Matlabプログラミングの問題が出されて、答えを書くとその長さに応じて得点が入る。短いほど高得点らしい。
http://www.mathworks.com/matlabcentral/cody/
今日はこれを考えてみる(ソース)。
http://www.mathworks.com/matlabcentral/cody/
今日はこれを考えてみる(ソース)。
INSTRUCTIONS
This is a multi-dimensional variant of the normal multiplication table used to teach elementary students multiplication. In this variant, we are going to produce a table that multiplies the divisors 1 to n (input) agains itself in d dimensions.
Note: Inputting d = 0 should return the number 1 and d = 1 should return a column vector with the elements 1 to n.
Example:
Input:
n = 3; d = 3;
Output:
tt(:,:,1) = [ 1 2 3
2 4 6
3 6 9 ];
tt(:,:,2) = [ 2 4 6
4 8 12
6 12 18 ];
tt(:,:,3) = [ 3 6 9
6 12 18
9 18 27 ];
PR
データフレームに長い名前を付けてしまうと、いちいち名前を指定するのが面倒くさい。
data.with.long.name <- data.frame(gdp=runif(10), price=runif(10))
data.with.long.name$gdppc <- data.with.long.name$gdp / data.with.long.name$price
with() を使うと、少しだけ楽になる。
data.with.long.name <- data.frame(gdp=runif(10), price=runif(10))
data.with.long.name$gdppc <- with(data.with.long.name, gdp / price)
within() というのもあって少し使いかたが違う。
data.with.long.name <- data.frame(gdp=runif(10), price=runif(10))
data.with.long.name <- within(data.with.long.name, gdppc <- gdp / price)
命令は複数書いても良いから、結構便利。
data.with.long.name <- data.frame(gdp=runif(10), price=runif(10))
data.with.long.name$gdppc <- data.with.long.name$gdp / data.with.long.name$price
with() を使うと、少しだけ楽になる。
data.with.long.name <- data.frame(gdp=runif(10), price=runif(10))
data.with.long.name$gdppc <- with(data.with.long.name, gdp / price)
within() というのもあって少し使いかたが違う。
data.with.long.name <- data.frame(gdp=runif(10), price=runif(10))
data.with.long.name <- within(data.with.long.name, gdppc <- gdp / price)
命令は複数書いても良いから、結構便利。
大した問題でもないが、pmlパッケージのpdata.frame関数に不具合発見。
どうも、「非欠損値が1つしかない」列があると困るらしい。
せっかくなのでcranプロジェクトにバグレポートしてみたら、これは「バグ」ではないとのこと。難しいもんだな。
どうも、「非欠損値が1つしかない」列があると困るらしい。
せっかくなのでcranプロジェクトにバグレポートしてみたら、これは「バグ」ではないとのこと。難しいもんだな。
library(plm)
dat <- data.frame(i = c(1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4),
t = c(1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3))
dat$x <- NA
dat$y <- NA
dat$z <- NA
dat$y[1] <- 1
dat$z[1:2] <- 2:3
dat
# this fails
pdata.frame(dat, index = c("i", "t"))
# this is fine
pdata.frame(dat[, -4], index = c("i", "t"))
sessionInfo()
以上だそうで。
ソース:http://r.789695.n4.nabble.com/Determine-package-version-in-R-td870896.html
出力例
以上だそうで。
ソース:http://r.789695.n4.nabble.com/Determine-package-version-in-R-td870896.html
出力例
> sessionInfo()
R version 2.13.2 (2011-09-30)
Platform: x86_64-pc-mingw32/x64 (64-bit)
locale:
[1] LC_COLLATE=English_United States.1252
[2] LC_CTYPE=English_United States.1252
[3] LC_MONETARY=English_United States.1252
[4] LC_NUMERIC=C
[5] LC_TIME=English_United States.1252
attached base packages:
[1] splines grid stats graphics grDevices utils
[7] datasets methods base
other attached packages:
[1] plm_1.2-8 nlme_3.1-102 bdsmatrix_1.3
[4] foreign_0.8-46 AER_1.1-9 strucchange_1.4-6
[7] sandwich_2.2-9 lmtest_0.9-29 zoo_1.7-6
[10] Formula_1.0-1 car_2.0-11 survival_2.36-9
[13] nnet_7.3-1 MASS_7.3-14 ggplot2_0.8.9
[16] proto_0.3-9.2 reshape_0.8.4 plyr_1.6
loaded via a namespace (and not attached):
[1] lattice_0.19-33 tools_2.13.2
どうもスクリプトの走りが悪いので、Rの計算速度をチェックしてみることにした。
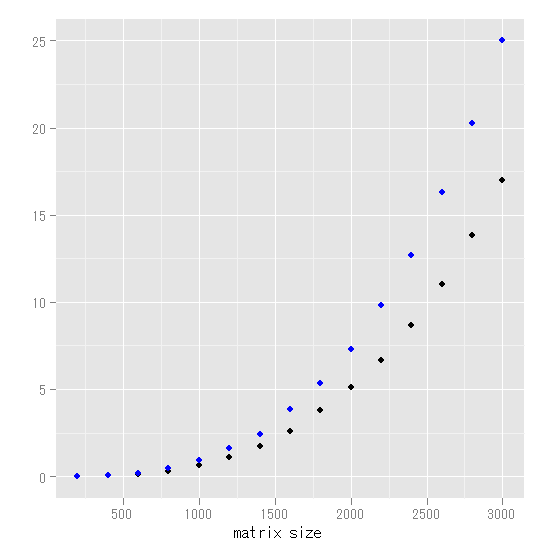
k * k の正方行列(正規分布) X を定義して、X' X を計算するという作業を、kの値を変えて行い、経過時間を調べる。Rではcrossprod関数を用いるか、t(X) %*% X という行列演算の2通りの方法がある。
下図は、横軸に行列のサイズ(k)を、縦軸に経過時間をプロットしたもの。黒がcrossprodを使った場合で、青は行列演算を使った場合。まず、相対的に見て、crossprodが圧倒的に早いことが目に付く。両者は全く同じ結果なので、行列演算は使わないほうがいいようだ。crosspordの方を見ると、2000*2000行列で5秒、3000*3000で17秒という結果だった。これ以降はちょっと時間が掛かりすぎるので止めた。
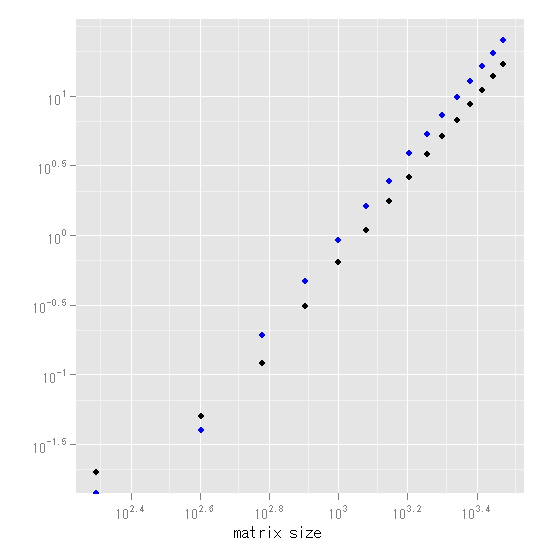
ただ、経過時間は結構正確に推計できる。上の図を、両対数を取った下の図を見てみると、ほぼ直線の関係になっていることが分かる。関係式を推計すると、
log(crossprod) = -18.83 + 2.69 log(size)
となる。例えば、サイズ6000を代入するとおよそ92秒と予測される。
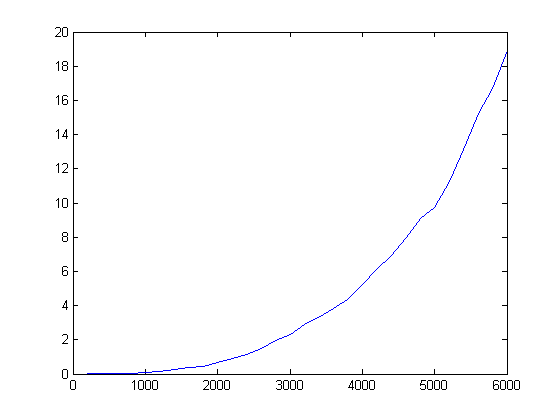
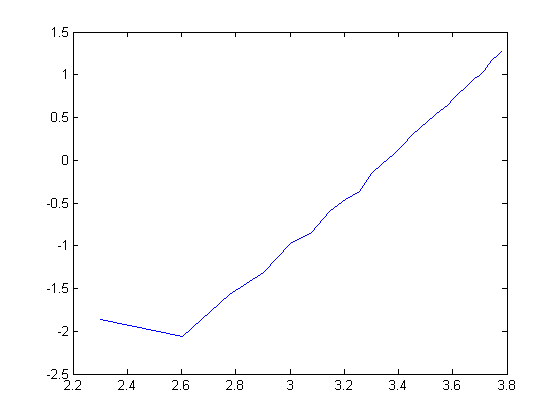
Matlabと比べるとRの遅さに驚く。サイズ2000で0.7秒、サイズ3000で2.3秒、サイズ6000で19秒だ。ちなみに、こちらも両対数を取ると直線になるから(サイズが小さい範囲は誤差だろう)、多分似たようなアルゴリズムではあるのかもしれない。関係式を推計してみると
log(time) = -19.59 + 2.55 log(size)
となり、比較的推計値の値が近い。
k * k の正方行列(正規分布) X を定義して、X' X を計算するという作業を、kの値を変えて行い、経過時間を調べる。Rではcrossprod関数を用いるか、t(X) %*% X という行列演算の2通りの方法がある。
下図は、横軸に行列のサイズ(k)を、縦軸に経過時間をプロットしたもの。黒がcrossprodを使った場合で、青は行列演算を使った場合。まず、相対的に見て、crossprodが圧倒的に早いことが目に付く。両者は全く同じ結果なので、行列演算は使わないほうがいいようだ。crosspordの方を見ると、2000*2000行列で5秒、3000*3000で17秒という結果だった。これ以降はちょっと時間が掛かりすぎるので止めた。
ただ、経過時間は結構正確に推計できる。上の図を、両対数を取った下の図を見てみると、ほぼ直線の関係になっていることが分かる。関係式を推計すると、
log(crossprod) = -18.83 + 2.69 log(size)
となる。例えば、サイズ6000を代入するとおよそ92秒と予測される。
Matlabと比べるとRの遅さに驚く。サイズ2000で0.7秒、サイズ3000で2.3秒、サイズ6000で19秒だ。ちなみに、こちらも両対数を取ると直線になるから(サイズが小さい範囲は誤差だろう)、多分似たようなアルゴリズムではあるのかもしれない。関係式を推計してみると
log(time) = -19.59 + 2.55 log(size)
となり、比較的推計値の値が近い。
Calender
| 01 | 2026/02 | 03 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Search in This Blog
Latest Comments
[03/30 川内のばば山田]
[03/30 川内のばば山田]
[08/06 Aterarie]
[07/05 Agazoger]
[07/01 Thomaskina]
Latest Posts
(11/16)
(04/28)
(04/16)
(04/11)
(04/05)
Latest Trackbacks
Category
Access Analysis

