Yaleで、遊んで学ぶ日々。
Yaleで、遊んで学ぶ日々。
囲碁、ときどきプログラミング、ところにより経済。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
今日のNHK杯(清成哲也九段 v 彦坂直人九段)で、解説の石田秀芳24世本因坊がトリビアを披露していた。
「黒が最後に駄目を詰めましたから、差は偶数ですね」
実際終わってみると黒が盤面8目勝っており、コミを入れて黒の1目半勝ちだった。
証明は簡単で、囲碁盤は19×19なのでもともと奇数個の目がある。一方、黒が先手だから、黒で打ち終えれば盤上に奇数個の石が置かれたことになる(アゲハマも結局は最後に地を埋めるのに使われる)。したがって、石のない部分は偶数個残っており、これを黒と白で分け合うので、その差は必ず偶数になる。逆もまた真。
* いずれかが着手放棄するという非常に稀なケースは例外。
置き碁の場合は、置き石が奇数個なら同様、偶数個なら関係が逆になる。
実戦においてまず役に立たない、まさに「トリビア」だが、一応、半目勝負がどちらに転ぶかが分かる。
『ヒカルの碁』の北斗杯日韓戦の時に、解説の渡辺先生が「細かい...これは整地してみないと...」と言っていたが、あれは実はこの理論を使えば判断できたわけだ。とはいえ、解説者が「今、白の高永夏君が最後の駄目を詰めたので白の半目勝ちですね」なんて言ったら興醒めか。
* 劇中ではコミ5目半なので、盤面奇数差の半目勝負なら盤面5目で白の勝ち。
「黒が最後に駄目を詰めましたから、差は偶数ですね」
実際終わってみると黒が盤面8目勝っており、コミを入れて黒の1目半勝ちだった。
証明は簡単で、囲碁盤は19×19なのでもともと奇数個の目がある。一方、黒が先手だから、黒で打ち終えれば盤上に奇数個の石が置かれたことになる(アゲハマも結局は最後に地を埋めるのに使われる)。したがって、石のない部分は偶数個残っており、これを黒と白で分け合うので、その差は必ず偶数になる。逆もまた真。
* いずれかが着手放棄するという非常に稀なケースは例外。
置き碁の場合は、置き石が奇数個なら同様、偶数個なら関係が逆になる。
実戦においてまず役に立たない、まさに「トリビア」だが、一応、半目勝負がどちらに転ぶかが分かる。
『ヒカルの碁』の北斗杯日韓戦の時に、解説の渡辺先生が「細かい...これは整地してみないと...」と言っていたが、あれは実はこの理論を使えば判断できたわけだ。とはいえ、解説者が「今、白の高永夏君が最後の駄目を詰めたので白の半目勝ちですね」なんて言ったら興醒めか。
* 劇中ではコミ5目半なので、盤面奇数差の半目勝負なら盤面5目で白の勝ち。
PR
「一目置く」というのは囲碁由来の慣用句。一目置く、つまり置き石をする、というのはハンデをもらうことなので、転じて相手との実力差を認め敬意を示すことを意味する。
10年くらい前に祖父と初めて囲碁を打ったときのこと(僕はルールも怪しいくらいの素人だった)。当然いくつも石を置かせていただいたのだが、祖父は「失礼して、白を持たせていただきます」と丁寧なご挨拶。石を置くのは必ず黒なので、置き碁なら白を持つのは必ず上手(うわて)。そういうわけで、「自分から白を持つ」というのは傲慢な印象を与えうるので、そこを緩和する意味で「持たせていただく」という日本風の礼儀が美しい。
今日テレビ放映されていた、第23回テレビ囲碁アジア選手権の中で、解説の高尾伸路九段が韓国のパク・ジョンファン九段を紹介する時に、「韓国のプロの間でも一目置かれる存在」と言っていたのがちょっと面白かった。プロ同士は互先で打っているので、現実には一目置いたりはしないのだが、語源を越えて使われる慣用句の楽しいところだ。
同様に、よいライバル関係にある二人が「互いに一目置いている」と言うことがあるが、これも本来はありえない。
10年くらい前に祖父と初めて囲碁を打ったときのこと(僕はルールも怪しいくらいの素人だった)。当然いくつも石を置かせていただいたのだが、祖父は「失礼して、白を持たせていただきます」と丁寧なご挨拶。石を置くのは必ず黒なので、置き碁なら白を持つのは必ず上手(うわて)。そういうわけで、「自分から白を持つ」というのは傲慢な印象を与えうるので、そこを緩和する意味で「持たせていただく」という日本風の礼儀が美しい。
今日テレビ放映されていた、第23回テレビ囲碁アジア選手権の中で、解説の高尾伸路九段が韓国のパク・ジョンファン九段を紹介する時に、「韓国のプロの間でも一目置かれる存在」と言っていたのがちょっと面白かった。プロ同士は互先で打っているので、現実には一目置いたりはしないのだが、語源を越えて使われる慣用句の楽しいところだ。
同様に、よいライバル関係にある二人が「互いに一目置いている」と言うことがあるが、これも本来はありえない。
【前回】
【年齢調整死亡率, 標準化死亡比:人口構成を調整する】
粗死亡率の弱点は、人口構成が異なる場合の比較が難しいところにある。そこで考え出されたのが年齢調整死亡率 (direct age-adjusted mortality rate, DAR) だ。DARは次のように定義される。
DAR(i) = Σ_k [ d(i,k) / n(i,k) ] * R(k)
k: 年齢グループ
d(i,k): 地域iにおけるグループkの死亡数
n(i,k):地域iにおけるグループkの人口
R(k): 標準人口構成におけるグループkの割合
式は多少複雑だが、理屈はシンプルだ。まず、グループごとに死亡率を求める。DARは、「そのグループ別死亡率のもとで、仮に標準的な人口構成だったとした場合」の死亡率だ。だから、人口構成が標準人口構成と同一である場合(つまり n(i,k) / n(i) = R(k) )には、DARとCMRは一致する。
標準人口は何でも良い。厚生労働省では、今のところ昭和60年のモデル人口が用いられているようだ(→厚生労働省:年齢調整死亡率について)。
また、一般には年齢構成について調整されることが多いが、実際には人口をグルーピングする方法は何でも良い。性別や職業・産業構成などで調整するのも時に有用だろう。
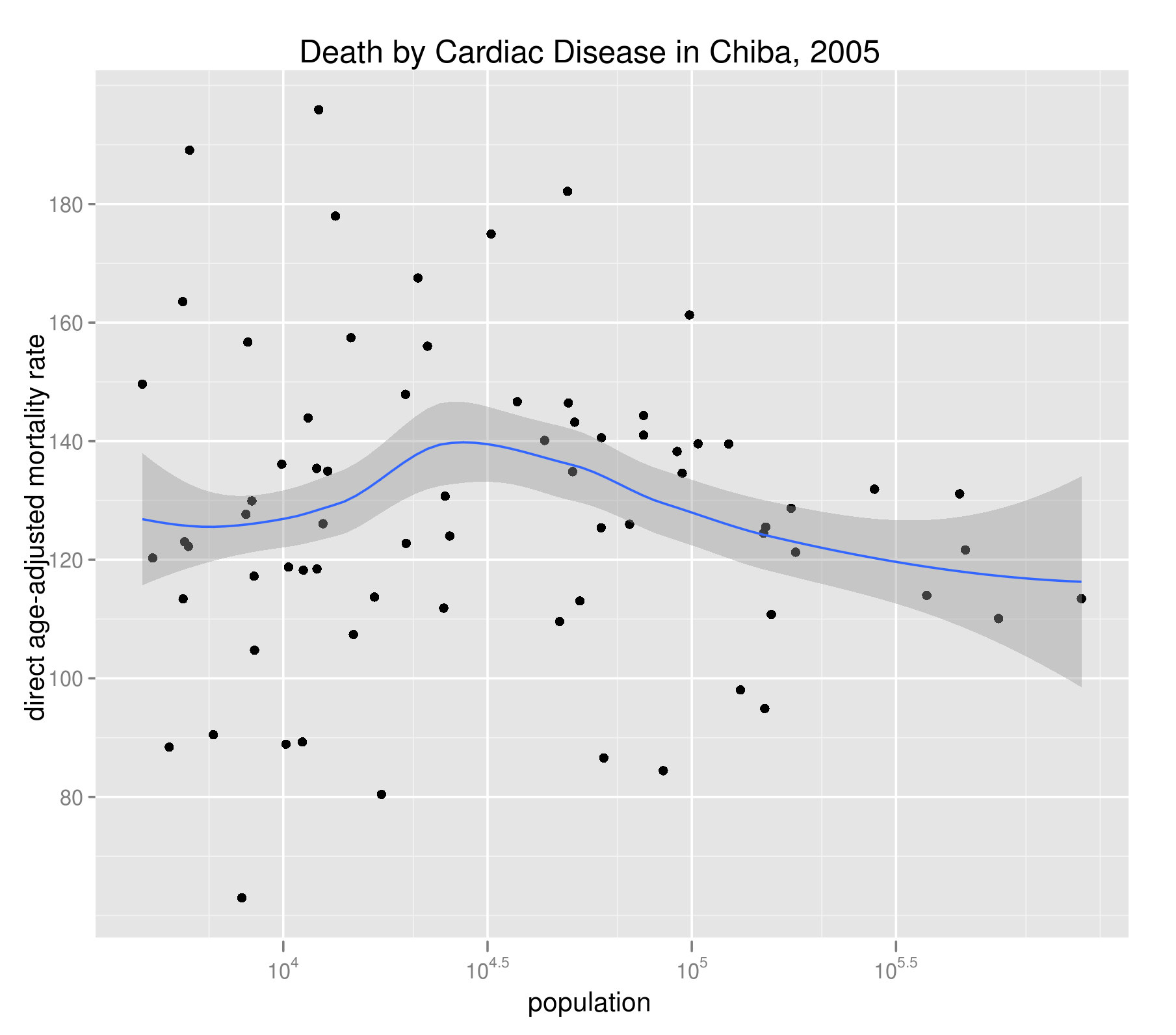
下図では、千葉県の心疾患(高血圧性を除く)による死亡について、性・年齢5歳階級グループで調整した各市町村のDARを人口とプロットしている。標準人口には、同年の千葉県全体の人口構成を用いた。CMRに見られたような負の相関が消えている。間接的ではあるが、CMRと人口規模の負の相関が人口構成を介する擬似相関であることを示唆している。
DARの1つの弱点は、詳細な死亡データが必要となる点である。グループ別の死亡者数(数式でのd(i,k))は、細かすぎて手に入らないことも多い。この点をカバーする代替指標の1つが、標準化死亡比(standardized mortality rate, SMR)だ。
SMR(i) = d(i) / Σ_k [ n(i,k) * P(k) ]
P(k): 標準的なグループkの死亡率
定義の分母は、標準的なグループkの死亡率と地域iの人口構成から計算される「予想死亡者数」となっており、SMRはその「予想死亡者数」が実際の死亡者数からどれだけ乖離しているかを表す指標だ。一般には、さらに100倍して100を基準とすることも多い。
SMRの1つの問題は、P(k)をどう定義するかだが、これには地域iの属する上位地域の死亡率を用いることが多い。例えば千葉県の市町村のSMRを計算する時には、千葉県全体の死亡率を用いるのが一案である。各都道府県のSMRの算出には日本全国の、各国のSMRの算出には世界全体の死亡率、といった具合だ。
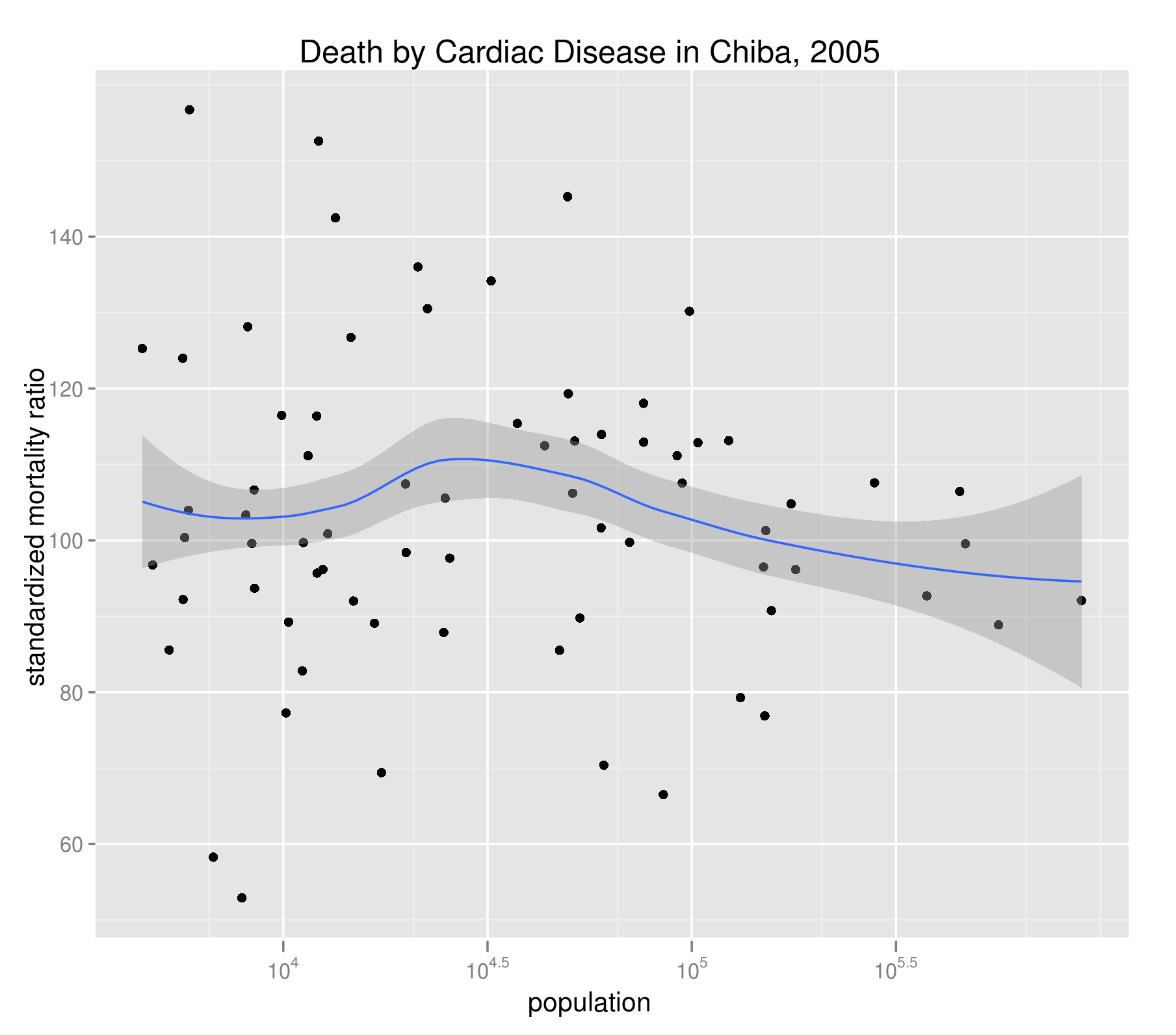
下図には、千葉県内の各市町村の心疾患(高血圧性を除く)に関するSMRとその人口の散布図を示した。グループ分けは、同じく性・年齢5歳階級で行っている。DARとよく似ており、人口構成による擬似相関はきっちり排除できている。
SMRの計算に必要な死亡データは地域別の総死亡数(d(i))だけなので、DARに比べてデータ面での要請は緩い。一方、その挙動はDARに近いのでなかなか優秀な指標のようだ。
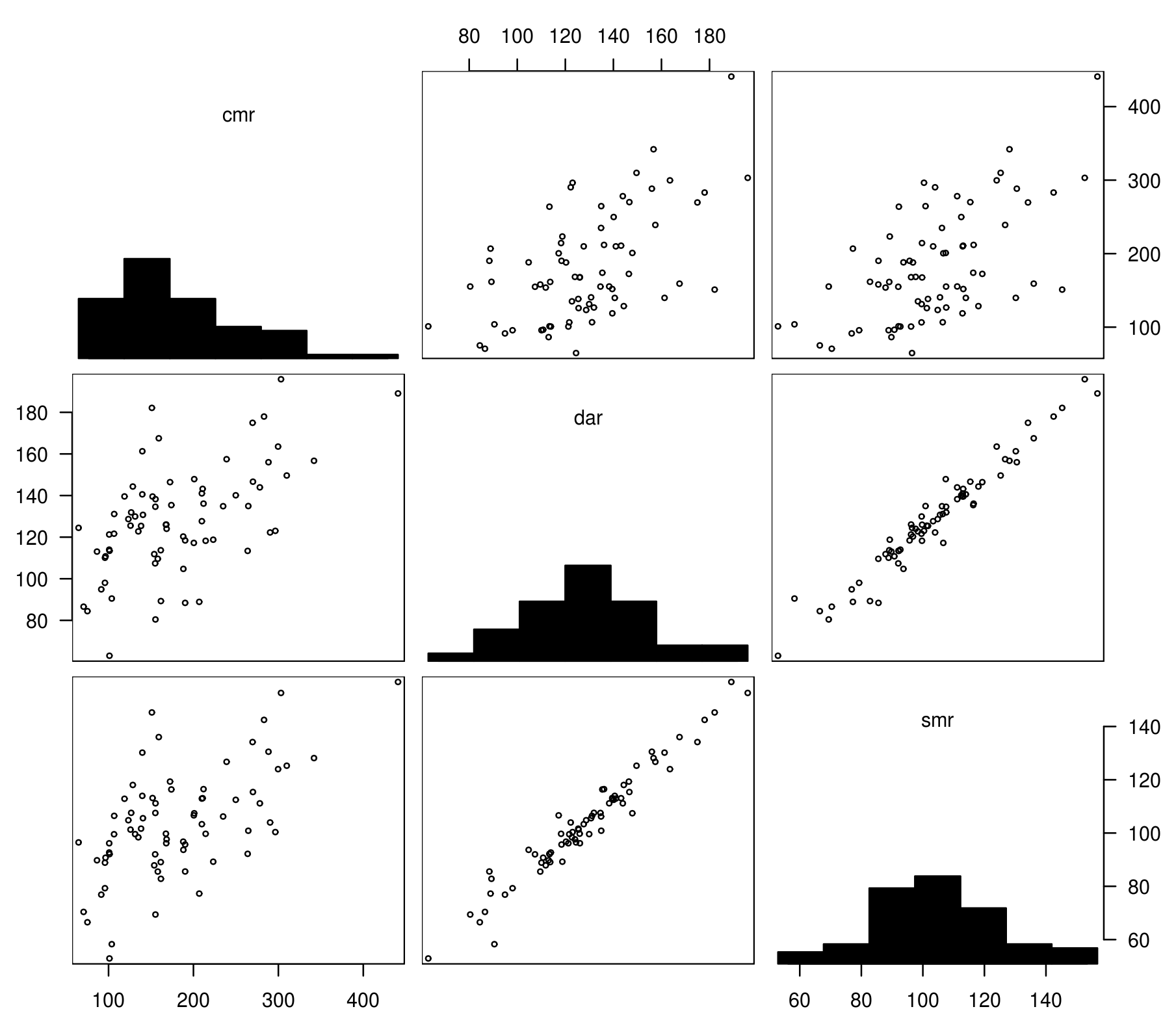
下図では、粗死亡率 (CMR), 年齢調整死亡率 (DAR), 標準化死亡比 (SMR) の3指標の関係を散布図に表した。DARとSMFの線形相関が極めて強く、一方CMRは他の指標とそこそこの相関を持つにすぎないことが分かる。
さて、死亡指標の比較には、年齢調整死亡率 (DAR) と 標準化死亡比 (SMR) の2つが非常によく用いられるが、それでも弱点がないわけではない。両指標の1つの弱点は、小地域における不安定性である。
先のグラフからも見て分かる通り、DARもSMRも、人口が小さくなるにつれて上下の振れ幅が大きくなっている(CMRも同様)。心疾患(高血圧性を除く)は比較的頻度の高い死因なので、一般には小規模地域における不安定性はもっと深刻になりうる。
端的に言えば、不安定性の原因はデータ不足にある。人口規模の小さい地域においては大数の法則が十分に成立しないため、死亡率が収束しきらないわけである。そこで、データ不足を補う方法を次に考える。
【つづき】
【年齢調整死亡率, 標準化死亡比:人口構成を調整する】
粗死亡率の弱点は、人口構成が異なる場合の比較が難しいところにある。そこで考え出されたのが年齢調整死亡率 (direct age-adjusted mortality rate, DAR) だ。DARは次のように定義される。
DAR(i) = Σ_k [ d(i,k) / n(i,k) ] * R(k)
k: 年齢グループ
d(i,k): 地域iにおけるグループkの死亡数
n(i,k):地域iにおけるグループkの人口
R(k): 標準人口構成におけるグループkの割合
式は多少複雑だが、理屈はシンプルだ。まず、グループごとに死亡率を求める。DARは、「そのグループ別死亡率のもとで、仮に標準的な人口構成だったとした場合」の死亡率だ。だから、人口構成が標準人口構成と同一である場合(つまり n(i,k) / n(i) = R(k) )には、DARとCMRは一致する。
標準人口は何でも良い。厚生労働省では、今のところ昭和60年のモデル人口が用いられているようだ(→厚生労働省:年齢調整死亡率について)。
また、一般には年齢構成について調整されることが多いが、実際には人口をグルーピングする方法は何でも良い。性別や職業・産業構成などで調整するのも時に有用だろう。
下図では、千葉県の心疾患(高血圧性を除く)による死亡について、性・年齢5歳階級グループで調整した各市町村のDARを人口とプロットしている。標準人口には、同年の千葉県全体の人口構成を用いた。CMRに見られたような負の相関が消えている。間接的ではあるが、CMRと人口規模の負の相関が人口構成を介する擬似相関であることを示唆している。
DARの1つの弱点は、詳細な死亡データが必要となる点である。グループ別の死亡者数(数式でのd(i,k))は、細かすぎて手に入らないことも多い。この点をカバーする代替指標の1つが、標準化死亡比(standardized mortality rate, SMR)だ。
SMR(i) = d(i) / Σ_k [ n(i,k) * P(k) ]
P(k): 標準的なグループkの死亡率
定義の分母は、標準的なグループkの死亡率と地域iの人口構成から計算される「予想死亡者数」となっており、SMRはその「予想死亡者数」が実際の死亡者数からどれだけ乖離しているかを表す指標だ。一般には、さらに100倍して100を基準とすることも多い。
SMRの1つの問題は、P(k)をどう定義するかだが、これには地域iの属する上位地域の死亡率を用いることが多い。例えば千葉県の市町村のSMRを計算する時には、千葉県全体の死亡率を用いるのが一案である。各都道府県のSMRの算出には日本全国の、各国のSMRの算出には世界全体の死亡率、といった具合だ。
下図には、千葉県内の各市町村の心疾患(高血圧性を除く)に関するSMRとその人口の散布図を示した。グループ分けは、同じく性・年齢5歳階級で行っている。DARとよく似ており、人口構成による擬似相関はきっちり排除できている。
SMRの計算に必要な死亡データは地域別の総死亡数(d(i))だけなので、DARに比べてデータ面での要請は緩い。一方、その挙動はDARに近いのでなかなか優秀な指標のようだ。
下図では、粗死亡率 (CMR), 年齢調整死亡率 (DAR), 標準化死亡比 (SMR) の3指標の関係を散布図に表した。DARとSMFの線形相関が極めて強く、一方CMRは他の指標とそこそこの相関を持つにすぎないことが分かる。
さて、死亡指標の比較には、年齢調整死亡率 (DAR) と 標準化死亡比 (SMR) の2つが非常によく用いられるが、それでも弱点がないわけではない。両指標の1つの弱点は、小地域における不安定性である。
先のグラフからも見て分かる通り、DARもSMRも、人口が小さくなるにつれて上下の振れ幅が大きくなっている(CMRも同様)。心疾患(高血圧性を除く)は比較的頻度の高い死因なので、一般には小規模地域における不安定性はもっと深刻になりうる。
端的に言えば、不安定性の原因はデータ不足にある。人口規模の小さい地域においては大数の法則が十分に成立しないため、死亡率が収束しきらないわけである。そこで、データ不足を補う方法を次に考える。
【つづき】
分野を問わず、死亡データを扱う場面は多い。公衆衛生学では、伝染病による死亡率が重要な関心事項の1つであるし、開発学においては乳幼児死亡率が国の発展のバロメータの1つとみなされる。都市計画では交通事故死の頻度を議論することもあるだろうし、自殺率や殺人死亡率は100年前から社会学の中心テーマだ。
死亡データの比較には、様々な死亡指標が用いられる。単純に死亡者数を人口で割ったいわゆる死亡率から、数値計算を行わなければ計算できないような複雑なものまで多種多様である。それらの死亡指標を具体的に計算しながら勉強しよう、というのがこの記事の目的。
【データ】
ネット上を検索したところ、千葉県の死亡データが市町村レベルで細かく手に入ったので、これを使用する。今回は平成17年の市町村別・死因別・性別・年齢階級別の死亡数を選んだ(→ソース)。平成17年にしたのは、国勢調査年なので後々便利かと思っただけで、深い理由はない。対応する人口データには、「住民基本台帳に基づく人口、人口動態及び世帯数調査」を用いた。市町村別・性別・年齢階級別の人口の年次データがe-statで手に入る(トップページから、「政府統計全体から探す」 >> 統計分野別「人口・世帯」 >> 「住民基本台帳に基づく人口、人口動態及び世帯数調査」 )。平成17年中の市町村合併を反映して、両データをマッチングする際には、夷隅町・大原町・岬町の3つをいすみ市に、干潟町・海上町・飯岡町の3つを旭市に計上した(→合併情報)。
【粗死亡率:人口規模を調整する】
死亡データを比較する時、死者数そのものを比べることにはほとんどの場合に意味がない。母数人口の規模が通常一定ではないからだ。言うまでもなく、人が多くいればそれだけ多くの死者が出やすいのだから、人口の差を加味しない比較はアンフェアである。
人口規模の違いを調整するために、死者数を母数人口で割ったものを「粗死亡率 (crude mortality rate, CMR)」と呼ぶ。小数点以下にゼロが並ぶと格好悪いので、10万をかけて「人口10万人あたり死亡者数」として計算するのが一般的。
CMR(i) = d(i) / n(i)
i: 地域
d(i): 地域iの死亡数
n(i): 地域iの人口
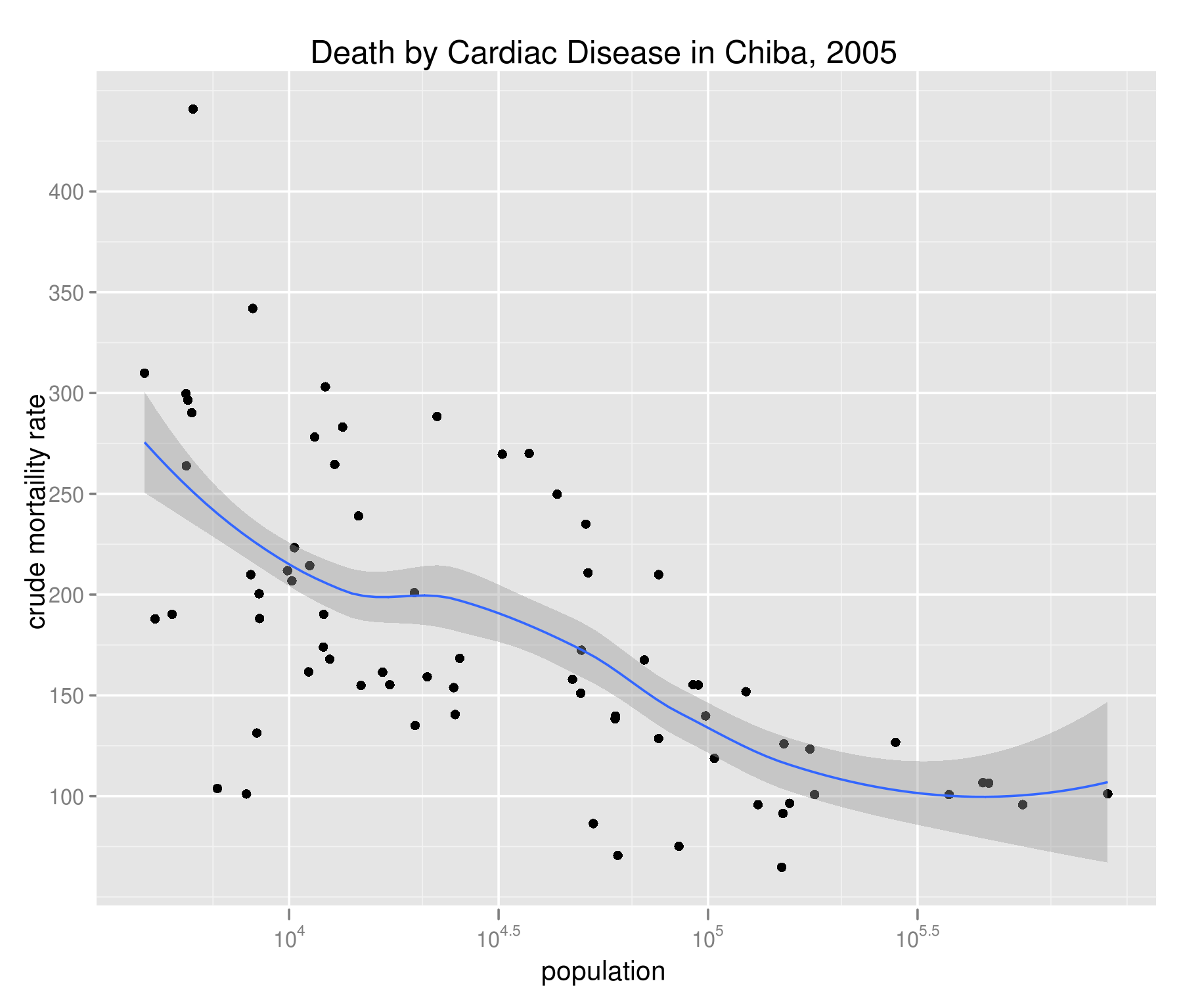
下図は、千葉県の各市町村について、心疾患(高血圧性を除く)による粗死亡率を求め、人口との散布図を描いたもの。強い負の相関が確認できる。なぜ負の相関なのか?
「人口規模が小さくなると心疾患のリスクが高まる」、と考えるのは早合点。これは典型的な擬似相関と見るべきだ。つまり、人口の小さいところは相対的に田舎で、高齢者の割合が大きく、そのため心疾患による死亡率が高くなるというわけだ。そういうわけで、千葉市と三芳村を比べるには、粗死亡率ではまだ不適格ということになる。人口規模の次は、人口構成の違いを調整する必要がある。
【つづき】
死亡データの比較には、様々な死亡指標が用いられる。単純に死亡者数を人口で割ったいわゆる死亡率から、数値計算を行わなければ計算できないような複雑なものまで多種多様である。それらの死亡指標を具体的に計算しながら勉強しよう、というのがこの記事の目的。
【データ】
ネット上を検索したところ、千葉県の死亡データが市町村レベルで細かく手に入ったので、これを使用する。今回は平成17年の市町村別・死因別・性別・年齢階級別の死亡数を選んだ(→ソース)。平成17年にしたのは、国勢調査年なので後々便利かと思っただけで、深い理由はない。対応する人口データには、「住民基本台帳に基づく人口、人口動態及び世帯数調査」を用いた。市町村別・性別・年齢階級別の人口の年次データがe-statで手に入る(トップページから、「政府統計全体から探す」 >> 統計分野別「人口・世帯」 >> 「住民基本台帳に基づく人口、人口動態及び世帯数調査」 )。平成17年中の市町村合併を反映して、両データをマッチングする際には、夷隅町・大原町・岬町の3つをいすみ市に、干潟町・海上町・飯岡町の3つを旭市に計上した(→合併情報)。
【粗死亡率:人口規模を調整する】
死亡データを比較する時、死者数そのものを比べることにはほとんどの場合に意味がない。母数人口の規模が通常一定ではないからだ。言うまでもなく、人が多くいればそれだけ多くの死者が出やすいのだから、人口の差を加味しない比較はアンフェアである。
人口規模の違いを調整するために、死者数を母数人口で割ったものを「粗死亡率 (crude mortality rate, CMR)」と呼ぶ。小数点以下にゼロが並ぶと格好悪いので、10万をかけて「人口10万人あたり死亡者数」として計算するのが一般的。
CMR(i) = d(i) / n(i)
i: 地域
d(i): 地域iの死亡数
n(i): 地域iの人口
下図は、千葉県の各市町村について、心疾患(高血圧性を除く)による粗死亡率を求め、人口との散布図を描いたもの。強い負の相関が確認できる。なぜ負の相関なのか?
「人口規模が小さくなると心疾患のリスクが高まる」、と考えるのは早合点。これは典型的な擬似相関と見るべきだ。つまり、人口の小さいところは相対的に田舎で、高齢者の割合が大きく、そのため心疾患による死亡率が高くなるというわけだ。そういうわけで、千葉市と三芳村を比べるには、粗死亡率ではまだ不適格ということになる。人口規模の次は、人口構成の違いを調整する必要がある。
【つづき】
Rでdata.frameを扱っているときに、ある変数の値ごとに何らかの操作をしたい、ということがよくある。例えば、次のような身長と性別のデータがあるとして、「性別ごとに平均を出したい」のようなことだ。
> dat
height gender
1 164.06 0
2 160.83 1
3 162.93 0
4 172.79 1
5 168.85 1
6 162.42 0
7 158.12 1
8 166.14 0
9 174.02 1
10 158.29 1
こういった操作は、by() 関数でできる。
> by(dat, dat$gender, mean)
dat$gender: 0
height gender
163.8875 0.0000
------------------------------------------------------------
dat$gender: 1
height gender
165.4833 1.0000
使い方は by(data, INDICES, FUN, ... ) で、
dataには対象となるdata.frame を、 INDICESには場合分けをするための変数を、FUNには使用する関数を与える。FUNの第1引数がdataの部分になり、FUNが他にも引数をとる場合には後に続ける。
例えばデータが欠損値を含んでいる場合、単にmean() で平均を出そうとすると欠損値が返ってくる。欠損値を無視するには、mean() を呼ぶ際に na.rm=T というオプションを加える。
> dat
height gender
1 164.06 0
2 160.83 1
3 NA 0
4 172.79 1
5 168.85 1
6 162.42 0
7 158.12 1
8 166.14 0
9 174.02 1
10 158.29 1
> by(dat, dat$gender, mean)
dat$gender: 0
height gender
NA 0
------------------------------------------------------------
dat$gender: 1
height gender
165.4833 1.0000
> by(dat, dat$gender, mean, na.rm=T)
dat$gender: 0
height gender
164.2067 0.0000
------------------------------------------------------------
dat$gender: 1
height gender
165.4833 1.0000
>
by() 関数の返り値は "by" というクラスなのだが、これはリストを継承する。したがって、インデックスで呼び出すなどの操作も可能。
> b <- by(dat, dat$gender, mean)
> b
dat$gender: 0
height gender
163.8875 0.0000
------------------------------------------------------------
dat$gender: 1
height gender
165.4833 1.0000
> names(b)
[1] "0" "1"
> b[[1]]
height gender
163.8875 0.0000
> b[["1"]]
height gender
165.4833 1.0000
> b$`0`
height gender
163.8875 0.0000
上の例では0と1の意味する所が無意味に分かりにくくなってしまっているが、b[[1]] はリストの第1要素(つまりgender:0に対する部分)、b[["1"]] はgender:1に対する部分、b$`0`はgender:0に対する部分を抜き出している。
ちなみに、無理矢理代入することも一応できるようだ。
> b[[1]] <- "replaced"
> b
dat$gender: 0
[1] "replaced"
------------------------------------------------------------
dat$gender: 1
height gender
165.4833 1.0000
> dat
height gender
1 164.06 0
2 160.83 1
3 162.93 0
4 172.79 1
5 168.85 1
6 162.42 0
7 158.12 1
8 166.14 0
9 174.02 1
10 158.29 1
こういった操作は、by() 関数でできる。
> by(dat, dat$gender, mean)
dat$gender: 0
height gender
163.8875 0.0000
------------------------------------------------------------
dat$gender: 1
height gender
165.4833 1.0000
使い方は by(data, INDICES, FUN, ... ) で、
dataには対象となるdata.frame を、 INDICESには場合分けをするための変数を、FUNには使用する関数を与える。FUNの第1引数がdataの部分になり、FUNが他にも引数をとる場合には後に続ける。
例えばデータが欠損値を含んでいる場合、単にmean() で平均を出そうとすると欠損値が返ってくる。欠損値を無視するには、mean() を呼ぶ際に na.rm=T というオプションを加える。
> dat
height gender
1 164.06 0
2 160.83 1
3 NA 0
4 172.79 1
5 168.85 1
6 162.42 0
7 158.12 1
8 166.14 0
9 174.02 1
10 158.29 1
> by(dat, dat$gender, mean)
dat$gender: 0
height gender
NA 0
------------------------------------------------------------
dat$gender: 1
height gender
165.4833 1.0000
> by(dat, dat$gender, mean, na.rm=T)
dat$gender: 0
height gender
164.2067 0.0000
------------------------------------------------------------
dat$gender: 1
height gender
165.4833 1.0000
>
by() 関数の返り値は "by" というクラスなのだが、これはリストを継承する。したがって、インデックスで呼び出すなどの操作も可能。
> b <- by(dat, dat$gender, mean)
> b
dat$gender: 0
height gender
163.8875 0.0000
------------------------------------------------------------
dat$gender: 1
height gender
165.4833 1.0000
> names(b)
[1] "0" "1"
> b[[1]]
height gender
163.8875 0.0000
> b[["1"]]
height gender
165.4833 1.0000
> b$`0`
height gender
163.8875 0.0000
上の例では0と1の意味する所が無意味に分かりにくくなってしまっているが、b[[1]] はリストの第1要素(つまりgender:0に対する部分)、b[["1"]] はgender:1に対する部分、b$`0`はgender:0に対する部分を抜き出している。
ちなみに、無理矢理代入することも一応できるようだ。
> b[[1]] <- "replaced"
> b
dat$gender: 0
[1] "replaced"
------------------------------------------------------------
dat$gender: 1
height gender
165.4833 1.0000
Calender
| 01 | 2026/02 | 03 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Search in This Blog
Latest Comments
[03/30 川内のばば山田]
[03/30 川内のばば山田]
[08/06 Aterarie]
[07/05 Agazoger]
[07/01 Thomaskina]
Latest Posts
(11/16)
(04/28)
(04/16)
(04/11)
(04/05)
Latest Trackbacks
Category
Access Analysis

