Yaleで、遊んで学ぶ日々。
Yaleで、遊んで学ぶ日々。
囲碁、ときどきプログラミング、ところにより経済。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
何でもランキングが出るとすぐにグラフを描きたくなるのは、職業病のようなものだ。仕事柄、混沌たるデータの中に一筋の秩序を見つけることを常に要求されるのだが、順位データは規則性が比較的見つかりやすく、気持ちいいのが特徴だ。
今夜は、ついさっき発表された第3回AKB48選抜総選挙の結果を少し眺めてみよう。数値はこのページから取得した。データはこちら。
下の2つの図はどちらも上位40名の得票数を上から並べて棒グラフにしたものだが、近似曲線の描き方だけが異なっている。1つ目はべき関数、2つ目は指数関数で近似している。決定係数はどちらも0.9を越えて優秀だが、若干指数近似の方が値が高い。どちらの近似曲線がより「正しそう」か、もう少し見てみよう。
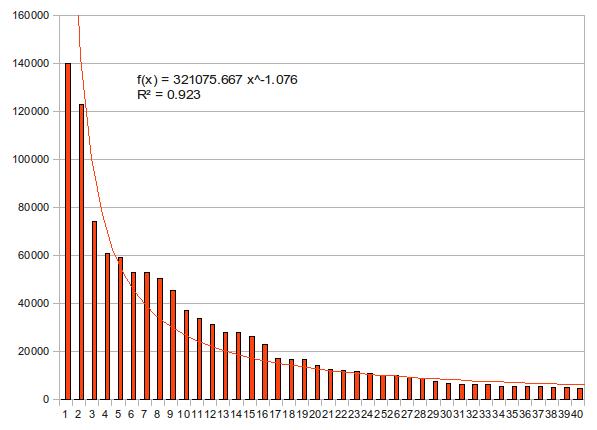
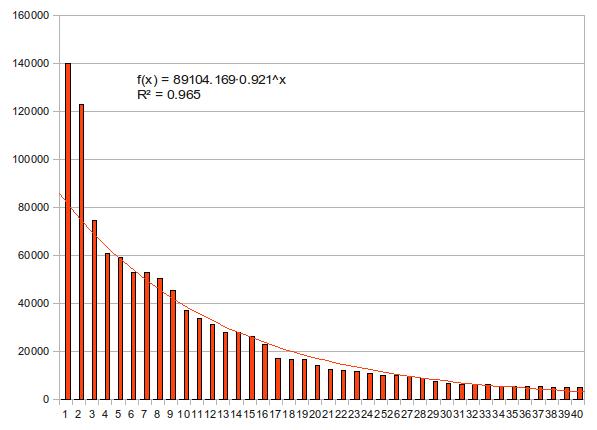
早稲田大学の西原先生は、微分方程式のゼミで、「人の目では直線くらいしか判断がつかない」と言っていた。曲線を見てそれがべき関数なのか指数関数なのかを判断するのは、人の知覚能力では困難だという教えだ(Yaleの同級生である戸田アレクシ哲が、あるグラフを見て「一目で双翼の指数分布だと気づいた」と言った時にはそのセンスに驚愕した)。非線形な関係にあるグラフを視覚的に判断するには、線形(ここではlinearではなくaffineの意)になるように上手いこと軸のスケールを変えるのが常用手段だ。
べき関数は、
y = a * x^r
という関係なので、両辺に対数を取ると
log(y) = C + r log(x)
C=log(a)
となる。そこで、x, yの両軸を対数にしたのが下図。
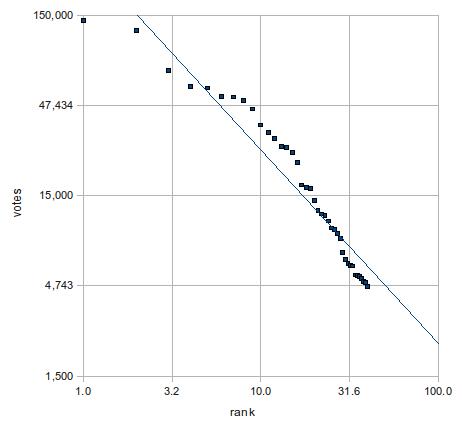
一方、指数近似では
y = a * b^x
という式に当てはめているので、
log(y) = C + D x
C =log(a), D=log(b)
つまり、片対数で直線になる。そこで下図ではy軸のみ対数にしてある。
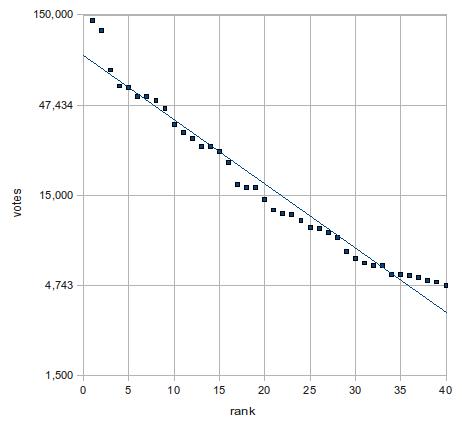
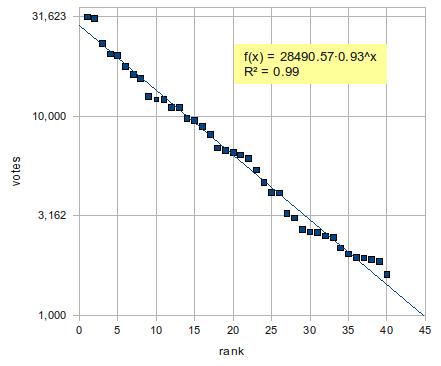
上の2つのグラフを比べれば、後者の近似がかなり有力であることは明らかだろう。ただし、上位2名(つまり、前田淳子と大島優子)は近似直線から大きくずれている。外れ値というやつだ。そこで、この2人を除いた3位から40位で改めて指数関数に当てはめてみよう。下図の通り、決定係数はさらに上がり、視覚的にもほぼ完璧に直線の上にデータが乗っている。
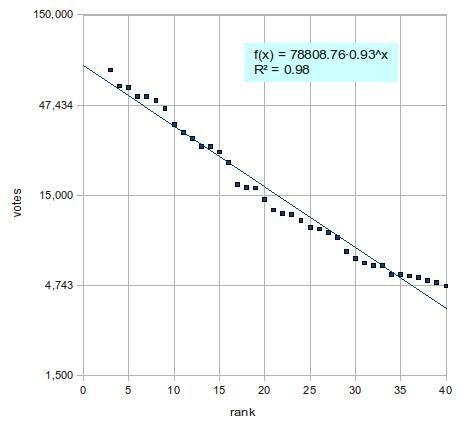
結論:第3回AKB48選抜総選挙の得票数は、順位の指数関数である。ただし、上位2人は外れ値。
上位2人だけが大きく外れる理由ははっきりとは分からないが、センターポジションに特別な意味があるということだろうか。
【つづき】
【追記】
昨年のデータで同じことをやったところ、同様に指数関数の当てはまりが極めて良く、かつ上位2人はやや外れ値だった。2回連続でこれなら偶然ではなさそうだ。何か、こういう分布を生じさせるメカニズムが存在すると見て間違いない。データはこちら。
今夜は、ついさっき発表された第3回AKB48選抜総選挙の結果を少し眺めてみよう。数値はこのページから取得した。データはこちら。
下の2つの図はどちらも上位40名の得票数を上から並べて棒グラフにしたものだが、近似曲線の描き方だけが異なっている。1つ目はべき関数、2つ目は指数関数で近似している。決定係数はどちらも0.9を越えて優秀だが、若干指数近似の方が値が高い。どちらの近似曲線がより「正しそう」か、もう少し見てみよう。
早稲田大学の西原先生は、微分方程式のゼミで、「人の目では直線くらいしか判断がつかない」と言っていた。曲線を見てそれがべき関数なのか指数関数なのかを判断するのは、人の知覚能力では困難だという教えだ(Yaleの同級生である戸田アレクシ哲が、あるグラフを見て「一目で双翼の指数分布だと気づいた」と言った時にはそのセンスに驚愕した)。非線形な関係にあるグラフを視覚的に判断するには、線形(ここではlinearではなくaffineの意)になるように上手いこと軸のスケールを変えるのが常用手段だ。
べき関数は、
y = a * x^r
という関係なので、両辺に対数を取ると
log(y) = C + r log(x)
C=log(a)
となる。そこで、x, yの両軸を対数にしたのが下図。
一方、指数近似では
y = a * b^x
という式に当てはめているので、
log(y) = C + D x
C =log(a), D=log(b)
つまり、片対数で直線になる。そこで下図ではy軸のみ対数にしてある。
上の2つのグラフを比べれば、後者の近似がかなり有力であることは明らかだろう。ただし、上位2名(つまり、前田淳子と大島優子)は近似直線から大きくずれている。外れ値というやつだ。そこで、この2人を除いた3位から40位で改めて指数関数に当てはめてみよう。下図の通り、決定係数はさらに上がり、視覚的にもほぼ完璧に直線の上にデータが乗っている。
結論:第3回AKB48選抜総選挙の得票数は、順位の指数関数である。ただし、上位2人は外れ値。
上位2人だけが大きく外れる理由ははっきりとは分からないが、センターポジションに特別な意味があるということだろうか。
【つづき】
【追記】
昨年のデータで同じことをやったところ、同様に指数関数の当てはまりが極めて良く、かつ上位2人はやや外れ値だった。2回連続でこれなら偶然ではなさそうだ。何か、こういう分布を生じさせるメカニズムが存在すると見て間違いない。データはこちら。
PR
Rによるディレクトリ・ファイル操作メモ
dir.create(): ディレクトリ作成。オプション recursive=TRUE を設定すれば階層のあるディレクトリ構造を作ることも可。
* pythonでいう os.mkdir(), os.makedirs()
file.exists(): ファイルやディレクトリの存在を確認。
* pythonでいう os.path.exists()
file.path(): パスの結合。
* pythonでいう os.path.join()
dir.create(): ディレクトリ作成。オプション recursive=TRUE を設定すれば階層のあるディレクトリ構造を作ることも可。
* pythonでいう os.mkdir(), os.makedirs()
file.exists(): ファイルやディレクトリの存在を確認。
* pythonでいう os.path.exists()
file.path(): パスの結合。
* pythonでいう os.path.join()
Rでは、chronパッケージのleap.year()関数を使って、ある年が閏年か否かを判定できる。
-----------------------------
> library(chron)
> leap.year(2011)
[1] FALSE
> leap.year(2008)
[1] TRUE
> leap.year(2000)
[1] TRUE
> leap.year(2100)
[1] FALSE
-----------------------------
2100年は閏年ではない。閏年になる条件を調べ直したところ、
(1) 原則 4で割りきれる年は閏年
(2) ただし 100で割りきれる年は閏年でない
(3) ただし 400で割りきれる年は閏年
だそうだ。そういえばそんな話を高校受験の英語長文で読んだ記憶があるような。。
-----------------------------
> library(chron)
> leap.year(2011)
[1] FALSE
> leap.year(2008)
[1] TRUE
> leap.year(2000)
[1] TRUE
> leap.year(2100)
[1] FALSE
-----------------------------
2100年は閏年ではない。閏年になる条件を調べ直したところ、
(1) 原則 4で割りきれる年は閏年
(2) ただし 100で割りきれる年は閏年でない
(3) ただし 400で割りきれる年は閏年
だそうだ。そういえばそんな話を高校受験の英語長文で読んだ記憶があるような。。
Rでは、chronパッケージのday.of.week() 関数を使って、日付から曜日を得ることが出来る。
---------------------
> library(chron)
> day.of.week(month=6, day=6, year=2011)
[1] 1
---------------------
ちなみに、0: 日曜 1: 月曜 ... 6: 土曜.
---------------------
> library(chron)
> day.of.week(month=6, day=6, year=2011)
[1] 1
---------------------
ちなみに、0: 日曜 1: 月曜 ... 6: 土曜.
例えば番号1からループでファイルを作ったとして、
1.png, 2.png, ...., 99.png
となってみると、名前順で並べると(環境にもよるが)、
1.png, 10.png, 11.png,...
というように、きちんと番号順にならずに少しばかりイラっとなることがある。
python では、zfill() 関数を使えばこの問題はすっきりする。zfill() 関数は、文字数を指定すると文字列の空き部分に0を挿入してくれるちょい便利関数だ。
---------------------
'5'.zfill(3)
(結果) '005'
---------------------
これを使って001.png, 002.png, ... というファイル名にすれば、並び替えた時にきちんと番号順になるという仕掛け。ちなみに、文字列関数なので数値でなくても可能。
---------------------
'ab'.zfill(3)
(結果) '0ab'
---------------------
1.png, 2.png, ...., 99.png
となってみると、名前順で並べると(環境にもよるが)、
1.png, 10.png, 11.png,...
というように、きちんと番号順にならずに少しばかりイラっとなることがある。
python では、zfill() 関数を使えばこの問題はすっきりする。zfill() 関数は、文字数を指定すると文字列の空き部分に0を挿入してくれるちょい便利関数だ。
---------------------
'5'.zfill(3)
(結果) '005'
---------------------
これを使って001.png, 002.png, ... というファイル名にすれば、並び替えた時にきちんと番号順になるという仕掛け。ちなみに、文字列関数なので数値でなくても可能。
---------------------
'ab'.zfill(3)
(結果) '0ab'
---------------------
Calender
| 01 | 2026/02 | 03 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Search in This Blog
Latest Comments
[03/30 川内のばば山田]
[03/30 川内のばば山田]
[08/06 Aterarie]
[07/05 Agazoger]
[07/01 Thomaskina]
Latest Posts
(11/16)
(04/28)
(04/16)
(04/11)
(04/05)
Latest Trackbacks
Category
Access Analysis

