2012/08/17 (Fri) 間違い探し

前の記事の終盤。互先の白。
黒の大石の死活が問題。実戦は、下図のようにコウになった。
1から6まで応手にいくつ間違いがあるだろうか。

 

そもそも下図白1に飛び込めば死んでいるじゃないか。


























上図黒6を下図のようにハサミツケても駄目。



























次に、白△のオサエに対して、下図黒1のカケツギで生きている。白2のハネ出しには問題集でお馴染みの切る手が成立している。


























白2で下図のサガリなら、反対側にハネカケツいで無事。



























さらに、黒△の時に、白1のカミトリで黒死。



























最後に、白△に対しては黒1で生きている。なぜ見えない。

おまけ：左下の黒も白から打つと死ぬ。おそらくお互いに対局中には見えてなかった。

























 

2012/08/17 (Fri) 死活

KGS対局から。互先の白。

白が△に押さえたところ。黒はどうする？

 

予想していたのは黒1からコウ。






























しかし実戦は黒△のツナギ。






























普通はハネ・ハネ・オキで5目中手だが、黒6にハサミツケられて困る。





























こっちからハネても。仮に黒2のサガリに受けざるを得ないとすると、黒に二眼を許してしまう。




























とすると、白1を効かして右下に戻るくらいだろうか。

 

2012/08/14 (Tue) 危険

久しぶりにKGSで対局。2子局の白。


結果的には快勝譜なんだけど、一カ所とんでもない読み間違いがあったので反省。

下図、S19のハネに白△に置いたのが咎められたら勝負が決まる嘘手。

 

黒の眼を取れるかな、と思って打ったオキ。黒がR19に受けてくれればバンザイだが、構わず黒1に押さえられるとあっさり白死。攻め取りにくらいはなるかもしれないけど、ひどい。




























下図白1のワリコミが良かったか。黒4まで決まればオキが成立。黒6に押さえられても直四目の生き。黒の眼形がもんだいだが、とりあえずP11あたりからでていけるのと、S10にツケ下がる筋で半眼ある。



























地に甘いが、オキに対して黒6についで白に渡らせれば黒は安心。万一封鎖されても将来黒Aに打てば黒生き。



























ちなみに、白1のワリコミに切るのは駄目のようだ。

 

2012/08/03 (Fri) 死活

最近、局後の検討を怠っていた。勝ち負けばかりに気を取られて、勝った碁を反省したり負けた碁から学んだりしないのは悪い兆候だと思う。

KGS対局から。コミなしの白。黒A, 白Bとなったところ。左上の白に厳しい手はあるか。

まずは2の1の急所から。白2に曲がれば無事。黒5には手抜きで生きている。後に黒7から白10となってセキ。





























黒1のツケの方が厳しいだろうか。渡られたらおしまいなので白2にハネて、黒3には白4でセキだろうか。

2012/07/20 (Fri) 一手の価値の計算

昨日行われた、第67期本因坊戦挑戦手合1日目のニコニコ生放送の中で、解説の大矢九段が出題したクイズ。

問題： A は何目の手か？

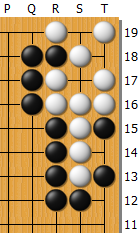
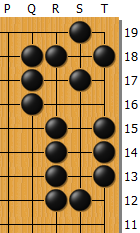
問題図は黒から打って本コウになる形。ここから変化して起こりうる図は、次の4通り。

状態1: 白が解消した形











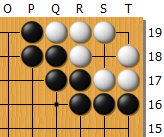
状態2: 問題図。黒から打って本コウ











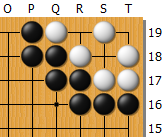
状態3: 白から打って本コウ











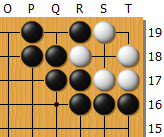
状態4: 黒が解消した形












このうち、状態1が白2目の地、状態4が黒13目の地（7目＋アゲハマ6)であることは数えれば分かる。そこで、黒の立場から考えて、
 V1 = -2
 V4 = 13
と書く。問題は状態2と3の価値はいくらか、ということだ。


結論から言うと、次のように素朴に考える。すなわち、状態1, 2, 3, 4 は等間隔である、と。すると、
 V2 = 3
 V3 = 8
でなくてはならない。
問題図のAの価値は、黒が打つならV2からV3への変化、白が打つなら V2からV1への変化であるから、いずれにしろ5目というのが答えになる（これは見合い計算の場合。出入り計算では10目と数える)。



さて、状態1〜4 はなぜ等間隔であると言えるのだろうか。これが、長い間の疑問だった。V2とV3の価値は、コウ材の具合に寄るではないのか。状態1〜4の価値が等間隔であるという考え方の裏には、どういう仮定が隠れているのか。次の命題がこの問いに答える。


命題：V1, V2, V3, V4が等間隔であるということと、状態2から状態1へ推移する確率が1/2であり、かつ状態3から状態4へ推移する確率が1/2である、ということは同値である。

証明：状態iから状態jへの推移確率をp(i, j)と書く。すると、次の連立方程式を得る。
V2 = p(2,1) * V1 + p(2,3) * V3
V3 = p(3,2) * V2 + p(3,4) * V4
ただし、確率の定義より、p(2,3) = 1 - p(2,1), p(3,2) = 1 - p(3,4)

もし、p(2,1) = 1/2, p(3,4) = 1/2であるなら、全ての推移確率は1/2になるので、上の方程式は
V2 = 2/3 * V1 + 1/3 * V4
V3 = 1/3 * V1 + 2/3 * V4
を導く。すなわち、V1, V2, V3, V4は等間隔である。

逆に、V1, V2, V3, V4が等間隔であるなら、方程式を解くことにより、
p(2,1) = 1/2
p(3,4) = 1/2
を得る。
【証明終】


というわけで、V1, V2, V3, V4が等間隔であるという考えの背後には、問題図においてAと打つのが黒になる確率と白になる確率が等しく、また状態3において、次にQ19に打つのが黒になる確率と白になる確率も等しい、という暗黙の仮定が隠れている。つまり、手番がランダムに巡ってくるという想定が、価値判断の核を構成している。


さて、本コウの場合、一般に、コウ争いにおける状態は4つある（白が解消、白がコウ取り、黒がコウ取り、黒が解消)。したがって、一手の価値を計算するには、白が解消した図と黒が解消した図の差を比べて、3で割ればいい（植木算。4点あれば、その間隔は3つ)。半コウを取る手が1/3目というのも同じ考え方による。


２段コウなら、状態が5つになるから、4で割って計算する。例えば下図は典型的な２段コウの形。ここから、白はT19, R19と2つ抜いて生き。一方黒は、S17, T14と抜いて取りきることができる。


















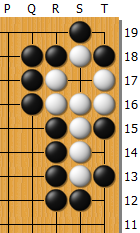
コウを解消した形は以下。左図では、白地が・・・5目くらい（黒Q19にはS19, 白T14には黒T12と決まるとすれば、白地3目＋アゲハマ3つ)？　一方、右図の黒地は・・・22目かな。計算方法が分かっても地を数えることができないんじゃ仕方がないな。まぁ大体そんなところだとして、解消形の差は27目。それを4で割って、一手の価値は7目弱、ということか（出入り計算で言えば14目弱)。合ってるのかな、これ。