Yaleで、遊んで学ぶ日々。
Yaleで、遊んで学ぶ日々。
囲碁、ときどきプログラミング、ところにより経済。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
文字列を大文字・小文字に変換するには、toupper(), tolower() 関数を使う。
> toupper("United States of America")
[1] "UNITED STATES OF AMERICA"
> tolower("I live in Tokyo, Japan")
[1] "i live in tokyo, japan"
> toupper("United States of America")
[1] "UNITED STATES OF AMERICA"
> tolower("I live in Tokyo, Japan")
[1] "i live in tokyo, japan"
PR
あるベクトルの累積和(第 j 要素がもとのベクトルの1~j 番までの和となるような同サイズのベクトル)を作りたいときは、cumsum() 関数を使う。
>cumsum(c(0,1,0,1,1,0))
[1] 0 1 1 2 3 3
> cumsum(c(0.1, 0.4, 0.2, 0.05, 0.15, 0.1))
[1] 0.10 0.50 0.70 0.75 0.90 1.00
>cumsum(c(0,1,0,1,1,0))
[1] 0 1 1 2 3 3
> cumsum(c(0.1, 0.4, 0.2, 0.05, 0.15, 0.1))
[1] 0.10 0.50 0.70 0.75 0.90 1.00
数年前からgmailを愛用している。大学のものを含めて複数のemailアカウントを持っているが、転送機能を使ってすべてgmailアカウントに集約している。代理送信機能を利用すれば、gmailで編集したメールを大学のアカウントを送信元として送ることもできる(ただし受け手によってはgmailを介して送られた旨が通知されることもある)。機能面において、大学のemailサービスでは日々進化を続けるフリーメールの足元も及ばない。Gmailで全て処理できるというのはとにかく快適だ。
Gmailは、容量もおよそ7GBと非常に充実しているが、重い添付ファイルなどが積み重なって、最近その半分ほどを使ってしまうにいたった。重要なファイルのバックアップとして、頻繁に添付ファイル付きのメールを送っているのが主たる原因のようだ。過去に遡っていくらか消去したが、重要度を判断するのが思いのほか難しかった(おそらくほとんど消しても困らないものだと思うが)。
そこで、新たにyahoo.comのメールアカウントを作成し、これをファイルバックアップ専用にすることにした。クリス・アンダーソンの『FREE: The Future of Radical Price』という本で知ったのだが、yahoo.comのフリーメールサービスは、容量が無制限だ。Gmailの台頭による勃発した価格競争の末、ベルトラン均衡点である価格ゼロにいち早く到達したという話だ。

保存しておきたいファイルが出来たら、gmailからyahoo mailへ添付で送る。ファイルの送り先という役割以外はすべて従来どおりGmailで行えば、今まで通り快適なemailライフが送れる。必要なファイルがある場合だけ、yahoo mailを開けばいい。ずっと使っていないとアカウント削除される、なんてことはないよね?
Gmailは、容量もおよそ7GBと非常に充実しているが、重い添付ファイルなどが積み重なって、最近その半分ほどを使ってしまうにいたった。重要なファイルのバックアップとして、頻繁に添付ファイル付きのメールを送っているのが主たる原因のようだ。過去に遡っていくらか消去したが、重要度を判断するのが思いのほか難しかった(おそらくほとんど消しても困らないものだと思うが)。
そこで、新たにyahoo.comのメールアカウントを作成し、これをファイルバックアップ専用にすることにした。クリス・アンダーソンの『FREE: The Future of Radical Price』という本で知ったのだが、yahoo.comのフリーメールサービスは、容量が無制限だ。Gmailの台頭による勃発した価格競争の末、ベルトラン均衡点である価格ゼロにいち早く到達したという話だ。

保存しておきたいファイルが出来たら、gmailからyahoo mailへ添付で送る。ファイルの送り先という役割以外はすべて従来どおりGmailで行えば、今まで通り快適なemailライフが送れる。必要なファイルがある場合だけ、yahoo mailを開けばいい。ずっと使っていないとアカウント削除される、なんてことはないよね?
AKB48得票数分析の最終回。
前々回の記事では、第3回選抜総選挙の得票数と順位の関係について、指数近似のフィットがかなり良いことを示し、前回の記事では得票数が順位の指数関数となるのは、得票数がlog-uniform分布に従う時であることを導いた。
今回はまとめとして、第1回から第3回までのデータを用いて、rank-frequency plot をもう一度よく見直し、議論を一旦締める。
データはこちら。ソースはここ。
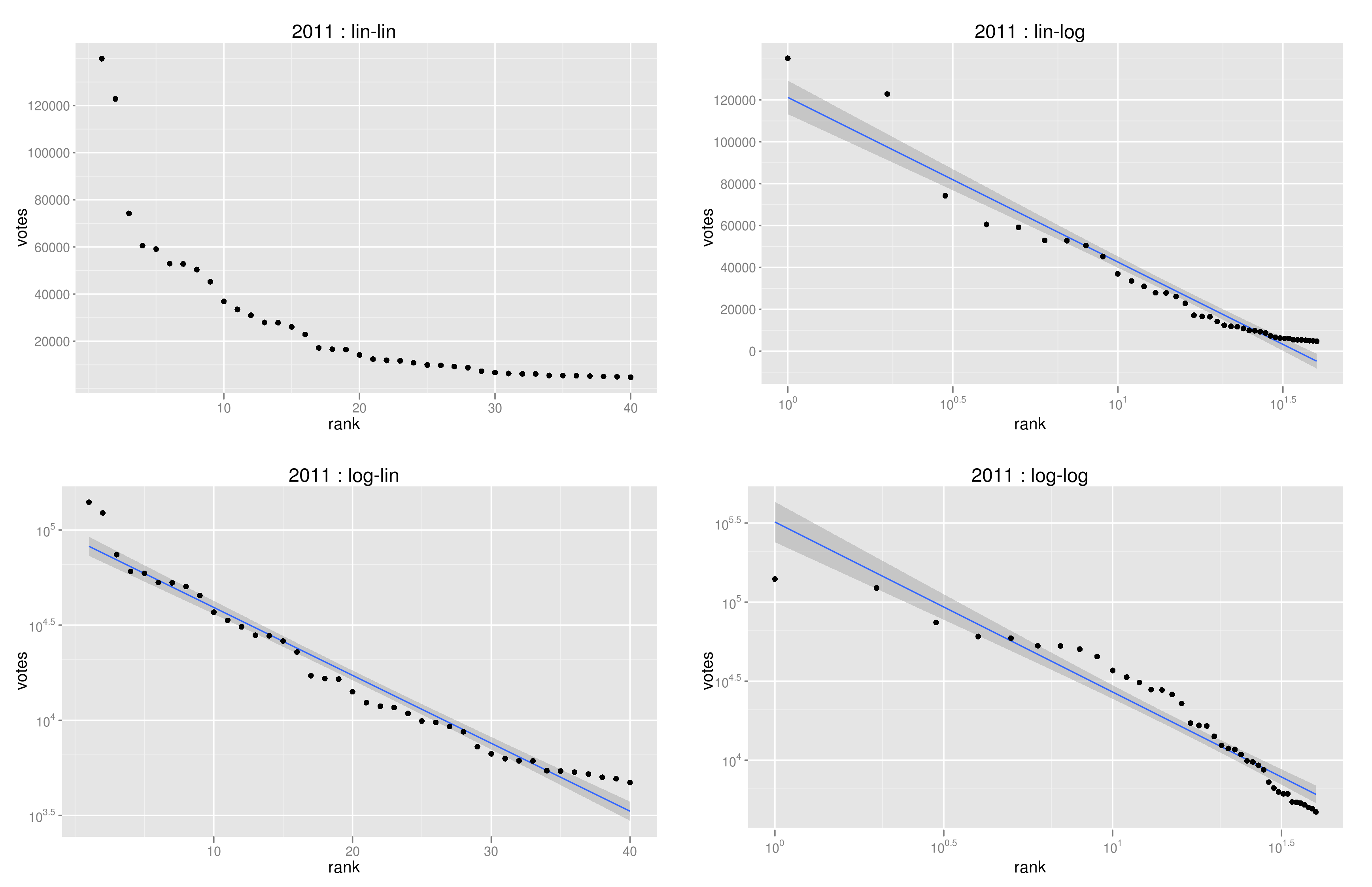
下図は、2011年のRank-frequency plotを4種類のスケールで描いたもの。lin-linは、両軸をそのままに、log-linはy軸を対数軸、lin-logはx軸を対数軸、log-logは両対数軸である。軸の取り方と得票数の分布の関係をまとめておくと
この図で比べてみると、やはりlog-lin(左下)の近似が一番良さそうに見える。
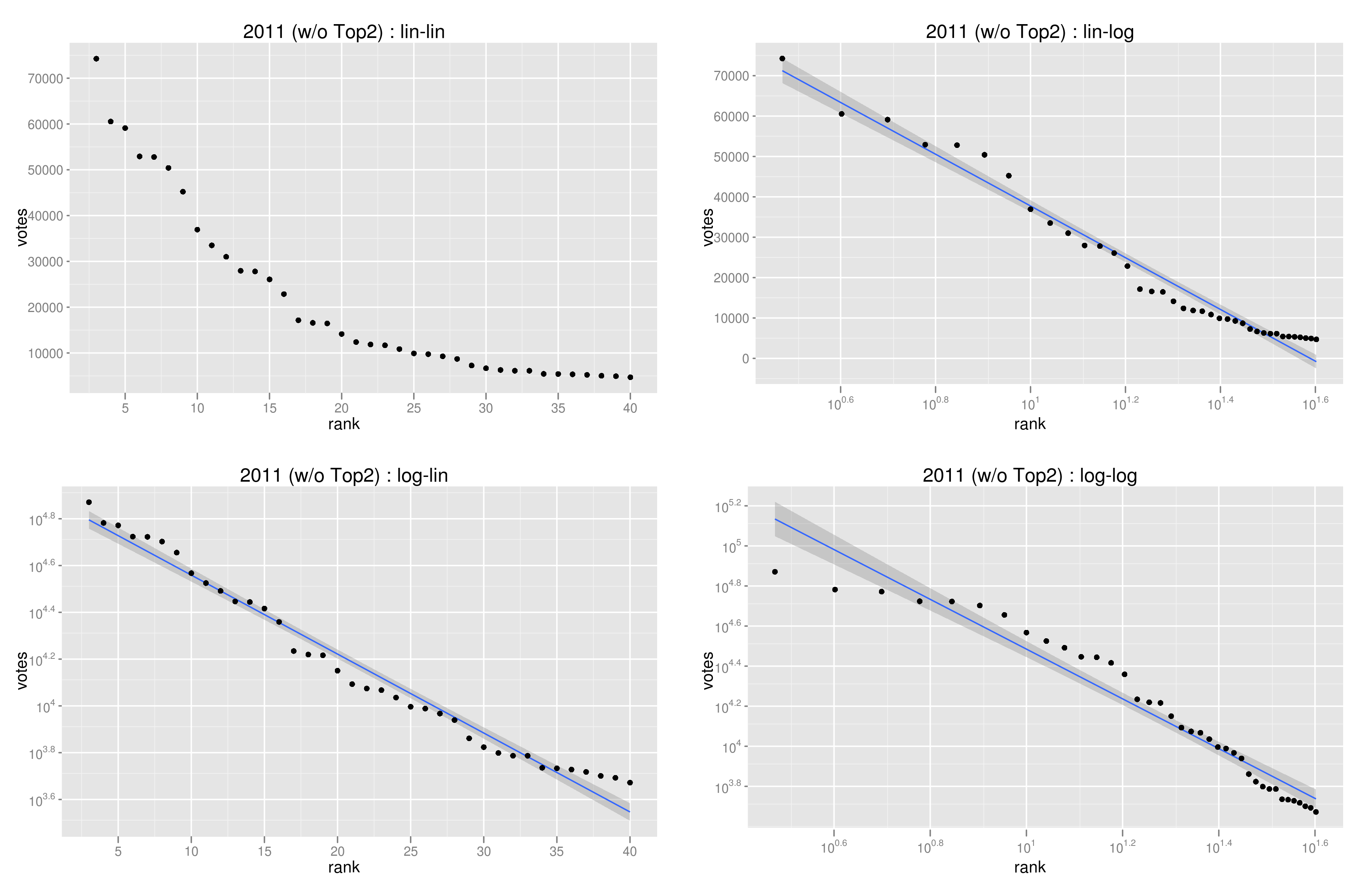
ただし、上位2名を除いて描き直してみると、結構難しいところ。これでも若干log-linが良さそうかな、と思う。
第1,2回ではさらに判断が難しい→2010年のグラフ, 2009年のグラフ。2010年ではlog-linとlin-logでともに綺麗な直線になっており、甲乙つけ難い。2009年では、むしろlog-logとlin-logがデッドヒートだ。総合すると、得票数の分布としてどれが一番有力であるかを視覚的に決めるのは難しい。統計的な検定をすることは理論的には可能だが、サンプルが30ないし40ではその力は限定的だろう。
実際のところ、1つの分布に限定する必要は必ずしもない。状況により、これらの分布の間を行ったり来たりするというのが答えかもしれない。たとえば、所得分布の研究では、高所得層ではパレート分布、中・低所得層では指数分布の当てはまりが良いことが知られている。ということは、何らかの要因でパレート分布に近くなったり指数分布に近くなったりする、というのもありそうな話だ。また、log-uniform分布とパレート分布は数学的には親戚関係にある。というのは、累積密度関数はそれぞれ
F(x) = a * log(x) + junk
F(x) = b * x^r + junk
であるので、これを微分して確率密度関数を求めると
f(x) ∝ x^(-1)
f(x) ∝ x^(r-1)
になる。つまり、パレート分布のパラメータ r をゼロに近づけていくと、だんだんとlog-uniform分布に近づいていくわけだ。
AKB48のことを調べて何になるかと言われれば全く何にもならないのだが、(AKBに限らず一般に)得票数の分布を真剣に分析した研究は少ないのではないかと思う。経済社会的な要因が政党の得票数にどう影響を与えるか、というのは政治経済学の王道トピックだが、得票数の分布に目を向けた話はあまり聞かない。もしかしたら、計量政治学の最も盛んな米国が二大政党制であるため、候補者数が2人の選挙が多くて分布も何もない、というのが原因かも(?)。他の国、例えば日本では政党数はそこそこあるし、小選挙区でも5人くらいの候補者がいる。知事選や地方議会選挙では数十人になることもある。するとそこには必然的に分布というものが発生するのである。
民主政治の根幹である「投票」について、分布から接近する手はないものか、とアイドルグループの人気投票を眺めながらそんなことを考えているのである。
【追記】
先行研究があった。1週間前の速報段階で全く同じことをやった人→YusukeMaedaさんのブログ。一年前の記事→ネット研。
前々回の記事では、第3回選抜総選挙の得票数と順位の関係について、指数近似のフィットがかなり良いことを示し、前回の記事では得票数が順位の指数関数となるのは、得票数がlog-uniform分布に従う時であることを導いた。
今回はまとめとして、第1回から第3回までのデータを用いて、rank-frequency plot をもう一度よく見直し、議論を一旦締める。
データはこちら。ソースはここ。
下図は、2011年のRank-frequency plotを4種類のスケールで描いたもの。lin-linは、両軸をそのままに、log-linはy軸を対数軸、lin-logはx軸を対数軸、log-logは両対数軸である。軸の取り方と得票数の分布の関係をまとめておくと
- lin-linで直線 ⇔ 一様分布
- log-linで直線 ⇔ log-uniform分布
- lin-logで直線 ⇔ 指数分布
- log-logで直線 ⇔ パレート分布
この図で比べてみると、やはりlog-lin(左下)の近似が一番良さそうに見える。
ただし、上位2名を除いて描き直してみると、結構難しいところ。これでも若干log-linが良さそうかな、と思う。
第1,2回ではさらに判断が難しい→2010年のグラフ, 2009年のグラフ。2010年ではlog-linとlin-logでともに綺麗な直線になっており、甲乙つけ難い。2009年では、むしろlog-logとlin-logがデッドヒートだ。総合すると、得票数の分布としてどれが一番有力であるかを視覚的に決めるのは難しい。統計的な検定をすることは理論的には可能だが、サンプルが30ないし40ではその力は限定的だろう。
実際のところ、1つの分布に限定する必要は必ずしもない。状況により、これらの分布の間を行ったり来たりするというのが答えかもしれない。たとえば、所得分布の研究では、高所得層ではパレート分布、中・低所得層では指数分布の当てはまりが良いことが知られている。ということは、何らかの要因でパレート分布に近くなったり指数分布に近くなったりする、というのもありそうな話だ。また、log-uniform分布とパレート分布は数学的には親戚関係にある。というのは、累積密度関数はそれぞれ
F(x) = a * log(x) + junk
F(x) = b * x^r + junk
であるので、これを微分して確率密度関数を求めると
f(x) ∝ x^(-1)
f(x) ∝ x^(r-1)
になる。つまり、パレート分布のパラメータ r をゼロに近づけていくと、だんだんとlog-uniform分布に近づいていくわけだ。
AKB48のことを調べて何になるかと言われれば全く何にもならないのだが、(AKBに限らず一般に)得票数の分布を真剣に分析した研究は少ないのではないかと思う。経済社会的な要因が政党の得票数にどう影響を与えるか、というのは政治経済学の王道トピックだが、得票数の分布に目を向けた話はあまり聞かない。もしかしたら、計量政治学の最も盛んな米国が二大政党制であるため、候補者数が2人の選挙が多くて分布も何もない、というのが原因かも(?)。他の国、例えば日本では政党数はそこそこあるし、小選挙区でも5人くらいの候補者がいる。知事選や地方議会選挙では数十人になることもある。するとそこには必然的に分布というものが発生するのである。
民主政治の根幹である「投票」について、分布から接近する手はないものか、とアイドルグループの人気投票を眺めながらそんなことを考えているのである。
【追記】
先行研究があった。1週間前の速報段階で全く同じことをやった人→YusukeMaedaさんのブログ。一年前の記事→ネット研。
前回の記事で、AKB48の総選挙得票数について、次のように結論づけた:
「第3回AKB48選抜総選挙の得票数は、順位の指数関数である」
実はこの文、当初は
「第3回AKB48選抜総選挙の得票数は、指数分布に従う」
となっていたのだが、ちょっと真偽が怪しいと思って書き直したのだ。
きちんと数式を解いたところ、やはりこの2つの文は同値ではないようだ。
前回の記事において、僕は、得票数と順位の関係を散布図に表し、それが指数関数でかなりよく近似できることを示した。この得票数と順位の散布図のことを rank-frequency plot という。この呼称は、この手の分析のパイオニアであるZiph先生が、シェイクスピア作品における単語の出現頻度(frequency)を分析したことに由来している(M.E.J. Newman, "Power laws, Pareto distributions and Zipf's law," Contemporary Physics 46(5), 2005 の Appendix Aを参照。→PDFへのリンク)。分析対象が変わっても rank-frequency plotと呼ぶのはややこしいことこの上ないのだが、とにかく、ここでfrequencyに該当するのは得票数であるということだ。
さて前回の結論を数式に表すと、
x = a * b^r .... (1)
x: 得票数, r: 順位
となる。簡単化のために、両辺に対数を取っておこう。
log(x) = C + D*r .... (1')
C=log(a), D=log(b)
今考えたいのは、「このようなrank-frequency plotを導くようなxの分布は何か」、ということだ。当初は考えもなしに「そりゃ指数分布だろ」と決め付けていたのだが、この第一感は怪しい。
x の累積密度関数をF(x)としよう。定義より、x よりも得票数の大きい人の割合は、1 - F(x) である。仮に母数をNとすれば、得票数 x の人の順位 r は、
r = [ 1 - F(x) ] * N .... (2)
と表せる。
したがって、(1'), (2)を用いてrを消去することにより
F(x) = α + β*log(x) .... (3)
α=1 + C/ND, β=-1/ND
を得る。
いくつか満たすべき条件がある。F(x)は0~1の値をとる単調増加関数なので、まずβ>0でなくてはいけない。また、xの値域は、 exp(-α/β) ≦ x ≦ exp((1-α)/β) である。
β>0の条件について考えておこう。定数の定義より、β>0 ⇔ D<0 ⇔ b∈(0,1) である。前回の記事でのbの値は0.9くらいだから、この条件を満たしている。
さて、(3) の分布はあまり見覚えのない式だが、どういう分布なのだろうか。y=log(x)と置くと見えやすいかもしれない(つまり yは得票数の自然対数)。するとy の累積密度関数 G は、
G(t) = Pr( y ≦ t ) = Pr( log(x) ≦ t ) = Pr( x ≦ exp(t) ) = F( exp(t) ) = α + β*t
と求められる。累積分布が一次関数、といえば答えは1つしかない:一様分布である。
結論: ある確率変数が log-uniform分布(対数を取ると一様分布)に従うならば、そのrank-frequency plot は指数関数になる。
百聞は一見に如かず。シミュレーションで確認してみよう(使用したRコード ggplot2パッケージが必要)。
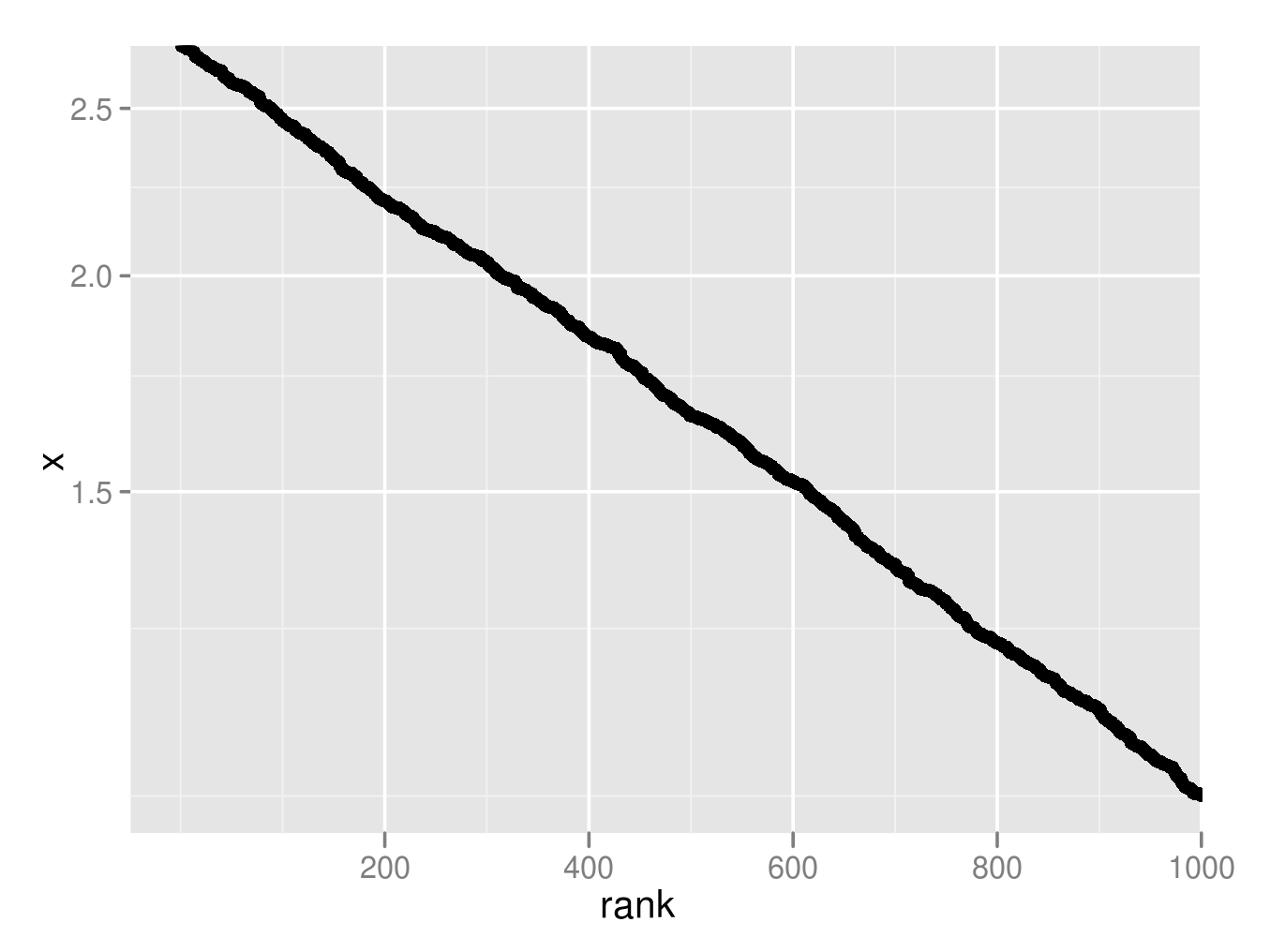
下図は、[0,1]区間の一様分布に従う乱数を1000個発生させ、そのexponentialをxとして、rank-frequency plotを描いたもの(y軸のみ対数軸)。綺麗な直線を描いており、上の議論の裏が取れた。
ちなみに、指数分布の rank-frequency plot はどうなるだろうか。どうも、対数を取るべき軸が逆転するようだ。というのも、計算すると分かるが、
x = a + b*log(r)
r: 順位
となるのである。
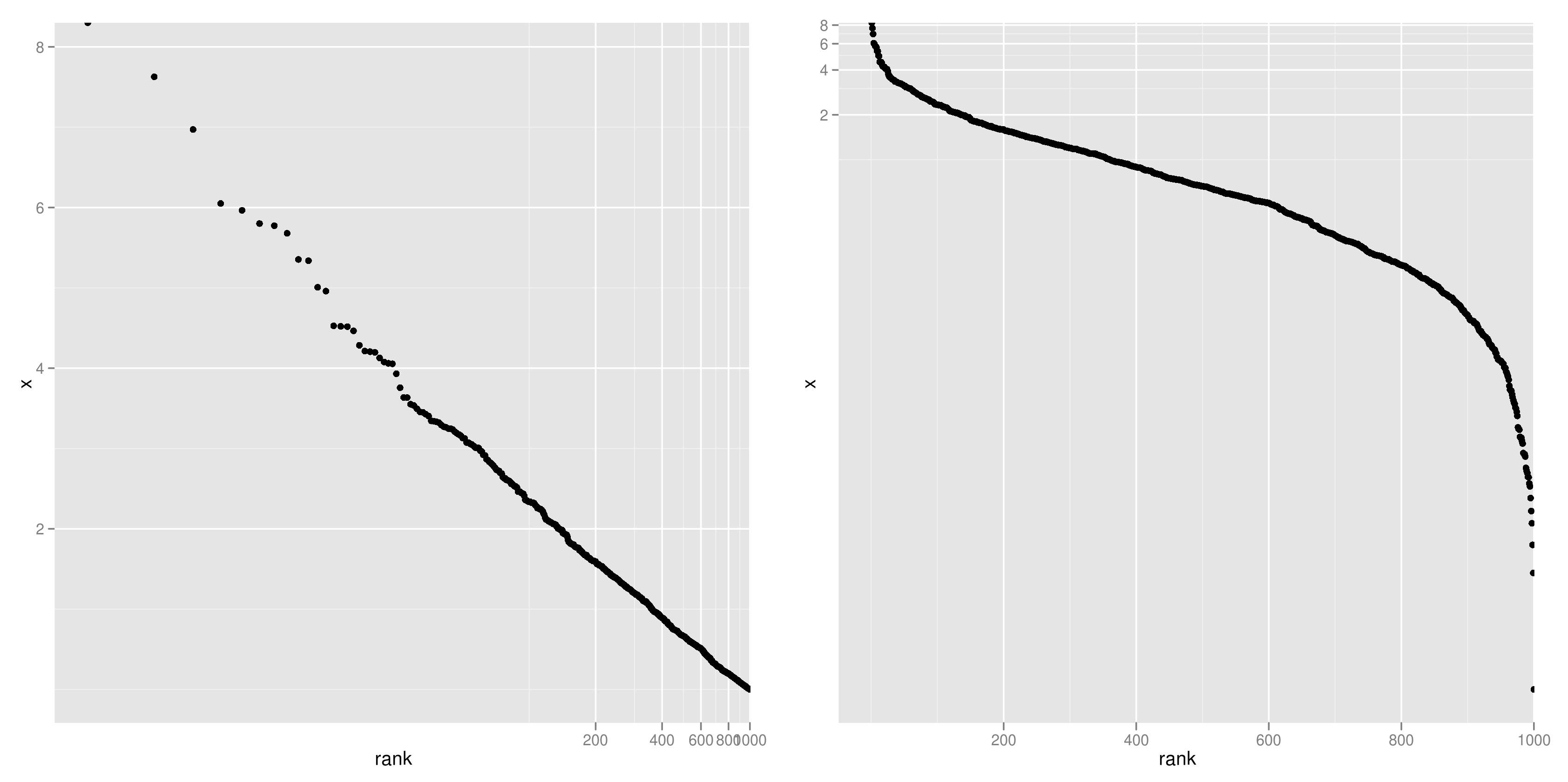
下図は、指数分布に従う乱数について rank-frequency plotを描いたものだが、順位にのみ対数を取る(左)と直線になることが分かる。一方、y軸のみを対数軸とする(右)とまるっきり直線にはならない。ゆえに、「第3回AKB48選抜総選挙の得票数は、指数分布に従う」は早とちりだったわけである。
というわけで、今回のAKB48の得票数分布については、log-uniformが有力候補である。なぜこの分布が現れるのか、という議論はかなり興味深いが、今のところビシッとした答えはでない。
【つづき】
「第3回AKB48選抜総選挙の得票数は、順位の指数関数である」
実はこの文、当初は
「第3回AKB48選抜総選挙の得票数は、指数分布に従う」
となっていたのだが、ちょっと真偽が怪しいと思って書き直したのだ。
きちんと数式を解いたところ、やはりこの2つの文は同値ではないようだ。
前回の記事において、僕は、得票数と順位の関係を散布図に表し、それが指数関数でかなりよく近似できることを示した。この得票数と順位の散布図のことを rank-frequency plot という。この呼称は、この手の分析のパイオニアであるZiph先生が、シェイクスピア作品における単語の出現頻度(frequency)を分析したことに由来している(M.E.J. Newman, "Power laws, Pareto distributions and Zipf's law," Contemporary Physics 46(5), 2005 の Appendix Aを参照。→PDFへのリンク)。分析対象が変わっても rank-frequency plotと呼ぶのはややこしいことこの上ないのだが、とにかく、ここでfrequencyに該当するのは得票数であるということだ。
さて前回の結論を数式に表すと、
x = a * b^r .... (1)
x: 得票数, r: 順位
となる。簡単化のために、両辺に対数を取っておこう。
log(x) = C + D*r .... (1')
C=log(a), D=log(b)
今考えたいのは、「このようなrank-frequency plotを導くようなxの分布は何か」、ということだ。当初は考えもなしに「そりゃ指数分布だろ」と決め付けていたのだが、この第一感は怪しい。
x の累積密度関数をF(x)としよう。定義より、x よりも得票数の大きい人の割合は、1 - F(x) である。仮に母数をNとすれば、得票数 x の人の順位 r は、
r = [ 1 - F(x) ] * N .... (2)
と表せる。
したがって、(1'), (2)を用いてrを消去することにより
F(x) = α + β*log(x) .... (3)
α=1 + C/ND, β=-1/ND
を得る。
いくつか満たすべき条件がある。F(x)は0~1の値をとる単調増加関数なので、まずβ>0でなくてはいけない。また、xの値域は、 exp(-α/β) ≦ x ≦ exp((1-α)/β) である。
β>0の条件について考えておこう。定数の定義より、β>0 ⇔ D<0 ⇔ b∈(0,1) である。前回の記事でのbの値は0.9くらいだから、この条件を満たしている。
さて、(3) の分布はあまり見覚えのない式だが、どういう分布なのだろうか。y=log(x)と置くと見えやすいかもしれない(つまり yは得票数の自然対数)。するとy の累積密度関数 G は、
G(t) = Pr( y ≦ t ) = Pr( log(x) ≦ t ) = Pr( x ≦ exp(t) ) = F( exp(t) ) = α + β*t
と求められる。累積分布が一次関数、といえば答えは1つしかない:一様分布である。
結論: ある確率変数が log-uniform分布(対数を取ると一様分布)に従うならば、そのrank-frequency plot は指数関数になる。
百聞は一見に如かず。シミュレーションで確認してみよう(使用したRコード ggplot2パッケージが必要)。
下図は、[0,1]区間の一様分布に従う乱数を1000個発生させ、そのexponentialをxとして、rank-frequency plotを描いたもの(y軸のみ対数軸)。綺麗な直線を描いており、上の議論の裏が取れた。
ちなみに、指数分布の rank-frequency plot はどうなるだろうか。どうも、対数を取るべき軸が逆転するようだ。というのも、計算すると分かるが、
x = a + b*log(r)
r: 順位
となるのである。
下図は、指数分布に従う乱数について rank-frequency plotを描いたものだが、順位にのみ対数を取る(左)と直線になることが分かる。一方、y軸のみを対数軸とする(右)とまるっきり直線にはならない。ゆえに、「第3回AKB48選抜総選挙の得票数は、指数分布に従う」は早とちりだったわけである。
というわけで、今回のAKB48の得票数分布については、log-uniformが有力候補である。なぜこの分布が現れるのか、という議論はかなり興味深いが、今のところビシッとした答えはでない。
【つづき】
Calender
| 01 | 2026/02 | 03 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Search in This Blog
Latest Comments
[03/30 川内のばば山田]
[03/30 川内のばば山田]
[08/06 Aterarie]
[07/05 Agazoger]
[07/01 Thomaskina]
Latest Posts
(11/16)
(04/28)
(04/16)
(04/11)
(04/05)
Latest Trackbacks
Category
Access Analysis

