Yaleで、遊んで学ぶ日々。
Yaleで、遊んで学ぶ日々。
囲碁、ときどきプログラミング、ところにより経済。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
前回の記事で、AKB48の総選挙得票数について、次のように結論づけた:
「第3回AKB48選抜総選挙の得票数は、順位の指数関数である」
実はこの文、当初は
「第3回AKB48選抜総選挙の得票数は、指数分布に従う」
となっていたのだが、ちょっと真偽が怪しいと思って書き直したのだ。
きちんと数式を解いたところ、やはりこの2つの文は同値ではないようだ。
前回の記事において、僕は、得票数と順位の関係を散布図に表し、それが指数関数でかなりよく近似できることを示した。この得票数と順位の散布図のことを rank-frequency plot という。この呼称は、この手の分析のパイオニアであるZiph先生が、シェイクスピア作品における単語の出現頻度(frequency)を分析したことに由来している(M.E.J. Newman, "Power laws, Pareto distributions and Zipf's law," Contemporary Physics 46(5), 2005 の Appendix Aを参照。→PDFへのリンク)。分析対象が変わっても rank-frequency plotと呼ぶのはややこしいことこの上ないのだが、とにかく、ここでfrequencyに該当するのは得票数であるということだ。
さて前回の結論を数式に表すと、
x = a * b^r .... (1)
x: 得票数, r: 順位
となる。簡単化のために、両辺に対数を取っておこう。
log(x) = C + D*r .... (1')
C=log(a), D=log(b)
今考えたいのは、「このようなrank-frequency plotを導くようなxの分布は何か」、ということだ。当初は考えもなしに「そりゃ指数分布だろ」と決め付けていたのだが、この第一感は怪しい。
x の累積密度関数をF(x)としよう。定義より、x よりも得票数の大きい人の割合は、1 - F(x) である。仮に母数をNとすれば、得票数 x の人の順位 r は、
r = [ 1 - F(x) ] * N .... (2)
と表せる。
したがって、(1'), (2)を用いてrを消去することにより
F(x) = α + β*log(x) .... (3)
α=1 + C/ND, β=-1/ND
を得る。
いくつか満たすべき条件がある。F(x)は0~1の値をとる単調増加関数なので、まずβ>0でなくてはいけない。また、xの値域は、 exp(-α/β) ≦ x ≦ exp((1-α)/β) である。
β>0の条件について考えておこう。定数の定義より、β>0 ⇔ D<0 ⇔ b∈(0,1) である。前回の記事でのbの値は0.9くらいだから、この条件を満たしている。
さて、(3) の分布はあまり見覚えのない式だが、どういう分布なのだろうか。y=log(x)と置くと見えやすいかもしれない(つまり yは得票数の自然対数)。するとy の累積密度関数 G は、
G(t) = Pr( y ≦ t ) = Pr( log(x) ≦ t ) = Pr( x ≦ exp(t) ) = F( exp(t) ) = α + β*t
と求められる。累積分布が一次関数、といえば答えは1つしかない:一様分布である。
結論: ある確率変数が log-uniform分布(対数を取ると一様分布)に従うならば、そのrank-frequency plot は指数関数になる。
百聞は一見に如かず。シミュレーションで確認してみよう(使用したRコード ggplot2パッケージが必要)。
下図は、[0,1]区間の一様分布に従う乱数を1000個発生させ、そのexponentialをxとして、rank-frequency plotを描いたもの(y軸のみ対数軸)。綺麗な直線を描いており、上の議論の裏が取れた。
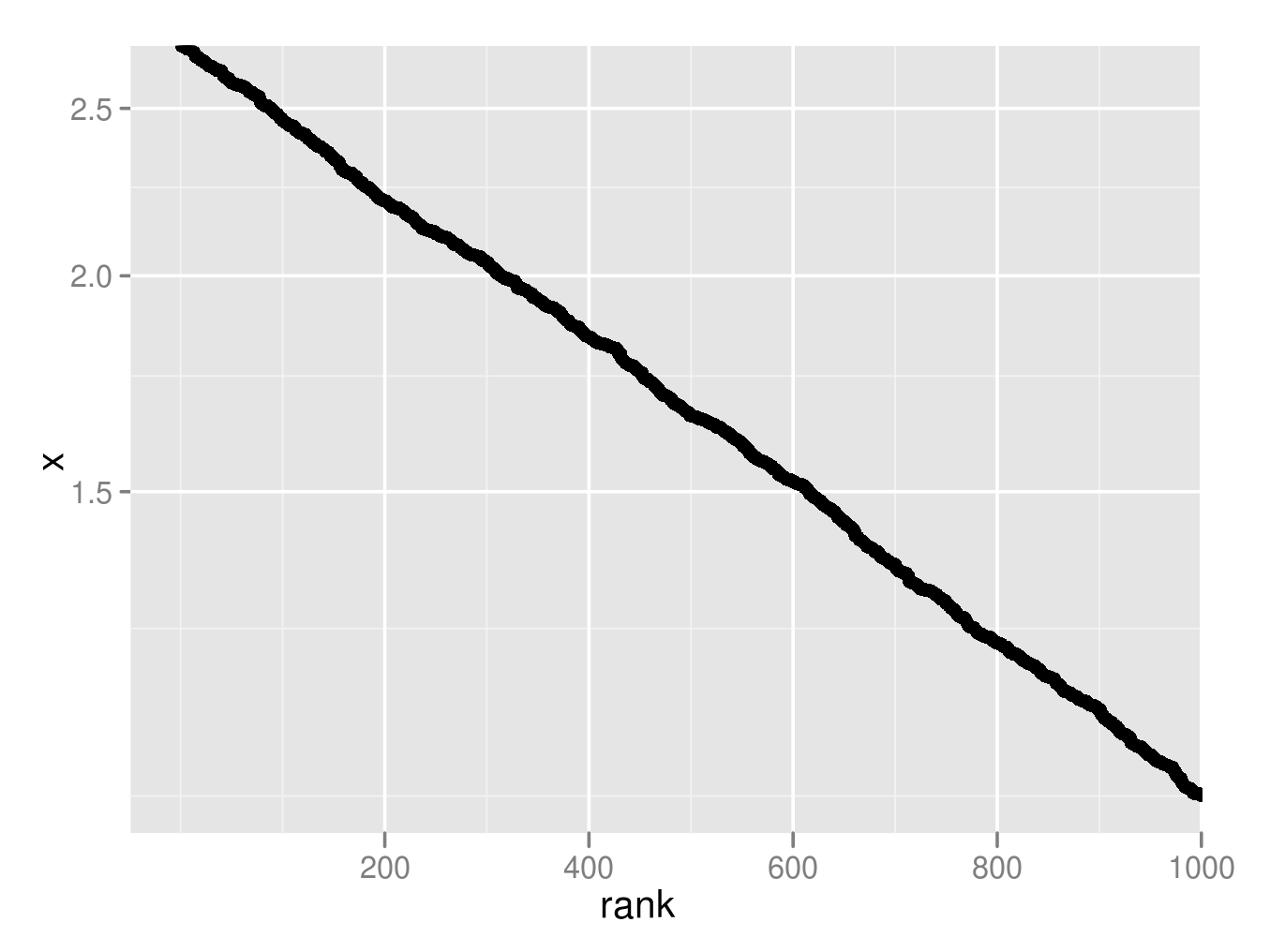
ちなみに、指数分布の rank-frequency plot はどうなるだろうか。どうも、対数を取るべき軸が逆転するようだ。というのも、計算すると分かるが、
x = a + b*log(r)
r: 順位
となるのである。
下図は、指数分布に従う乱数について rank-frequency plotを描いたものだが、順位にのみ対数を取る(左)と直線になることが分かる。一方、y軸のみを対数軸とする(右)とまるっきり直線にはならない。ゆえに、「第3回AKB48選抜総選挙の得票数は、指数分布に従う」は早とちりだったわけである。
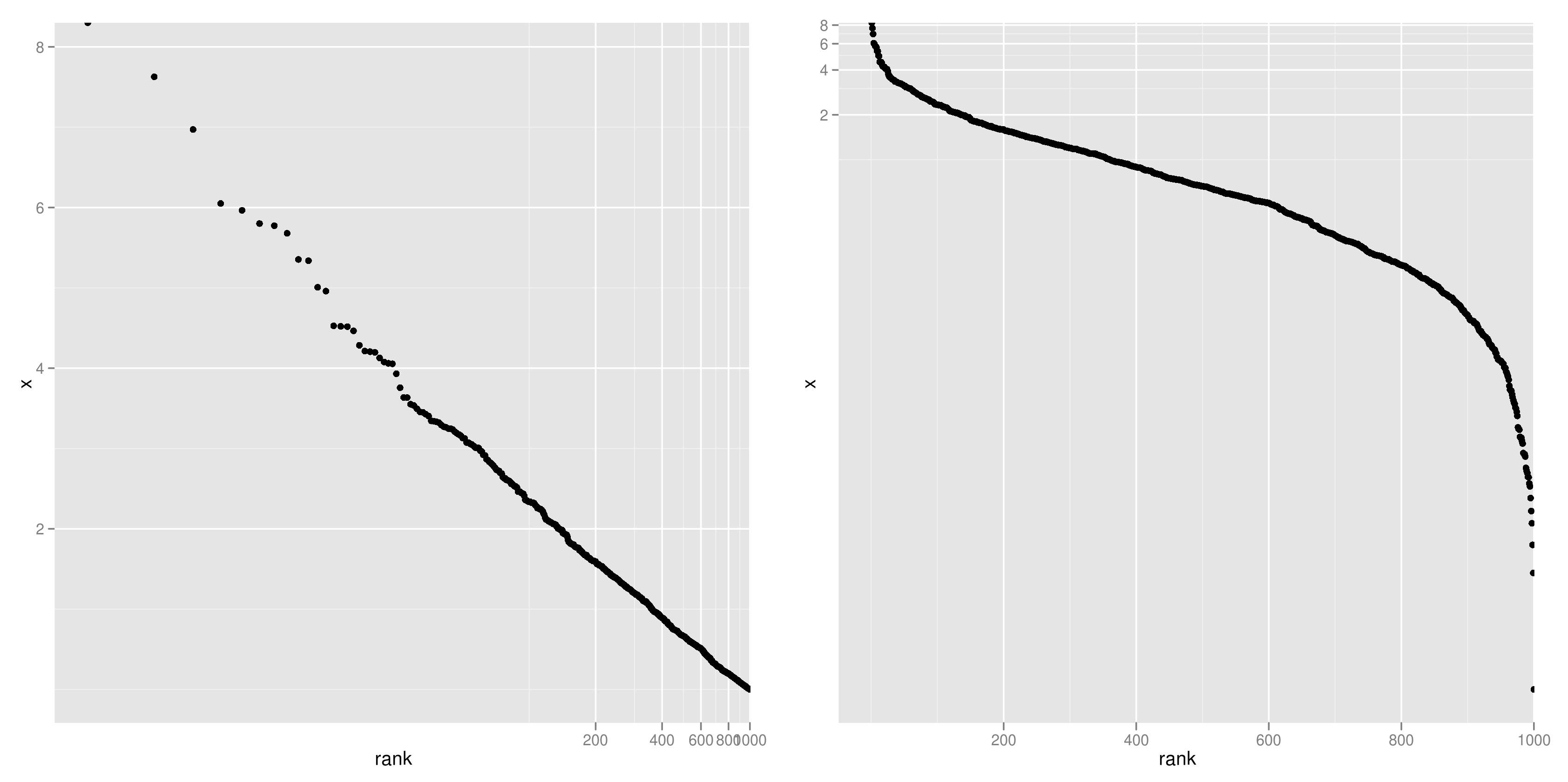
というわけで、今回のAKB48の得票数分布については、log-uniformが有力候補である。なぜこの分布が現れるのか、という議論はかなり興味深いが、今のところビシッとした答えはでない。
【つづき】
「第3回AKB48選抜総選挙の得票数は、順位の指数関数である」
実はこの文、当初は
「第3回AKB48選抜総選挙の得票数は、指数分布に従う」
となっていたのだが、ちょっと真偽が怪しいと思って書き直したのだ。
きちんと数式を解いたところ、やはりこの2つの文は同値ではないようだ。
前回の記事において、僕は、得票数と順位の関係を散布図に表し、それが指数関数でかなりよく近似できることを示した。この得票数と順位の散布図のことを rank-frequency plot という。この呼称は、この手の分析のパイオニアであるZiph先生が、シェイクスピア作品における単語の出現頻度(frequency)を分析したことに由来している(M.E.J. Newman, "Power laws, Pareto distributions and Zipf's law," Contemporary Physics 46(5), 2005 の Appendix Aを参照。→PDFへのリンク)。分析対象が変わっても rank-frequency plotと呼ぶのはややこしいことこの上ないのだが、とにかく、ここでfrequencyに該当するのは得票数であるということだ。
さて前回の結論を数式に表すと、
x = a * b^r .... (1)
x: 得票数, r: 順位
となる。簡単化のために、両辺に対数を取っておこう。
log(x) = C + D*r .... (1')
C=log(a), D=log(b)
今考えたいのは、「このようなrank-frequency plotを導くようなxの分布は何か」、ということだ。当初は考えもなしに「そりゃ指数分布だろ」と決め付けていたのだが、この第一感は怪しい。
x の累積密度関数をF(x)としよう。定義より、x よりも得票数の大きい人の割合は、1 - F(x) である。仮に母数をNとすれば、得票数 x の人の順位 r は、
r = [ 1 - F(x) ] * N .... (2)
と表せる。
したがって、(1'), (2)を用いてrを消去することにより
F(x) = α + β*log(x) .... (3)
α=1 + C/ND, β=-1/ND
を得る。
いくつか満たすべき条件がある。F(x)は0~1の値をとる単調増加関数なので、まずβ>0でなくてはいけない。また、xの値域は、 exp(-α/β) ≦ x ≦ exp((1-α)/β) である。
β>0の条件について考えておこう。定数の定義より、β>0 ⇔ D<0 ⇔ b∈(0,1) である。前回の記事でのbの値は0.9くらいだから、この条件を満たしている。
さて、(3) の分布はあまり見覚えのない式だが、どういう分布なのだろうか。y=log(x)と置くと見えやすいかもしれない(つまり yは得票数の自然対数)。するとy の累積密度関数 G は、
G(t) = Pr( y ≦ t ) = Pr( log(x) ≦ t ) = Pr( x ≦ exp(t) ) = F( exp(t) ) = α + β*t
と求められる。累積分布が一次関数、といえば答えは1つしかない:一様分布である。
結論: ある確率変数が log-uniform分布(対数を取ると一様分布)に従うならば、そのrank-frequency plot は指数関数になる。
百聞は一見に如かず。シミュレーションで確認してみよう(使用したRコード ggplot2パッケージが必要)。
下図は、[0,1]区間の一様分布に従う乱数を1000個発生させ、そのexponentialをxとして、rank-frequency plotを描いたもの(y軸のみ対数軸)。綺麗な直線を描いており、上の議論の裏が取れた。
ちなみに、指数分布の rank-frequency plot はどうなるだろうか。どうも、対数を取るべき軸が逆転するようだ。というのも、計算すると分かるが、
x = a + b*log(r)
r: 順位
となるのである。
下図は、指数分布に従う乱数について rank-frequency plotを描いたものだが、順位にのみ対数を取る(左)と直線になることが分かる。一方、y軸のみを対数軸とする(右)とまるっきり直線にはならない。ゆえに、「第3回AKB48選抜総選挙の得票数は、指数分布に従う」は早とちりだったわけである。
というわけで、今回のAKB48の得票数分布については、log-uniformが有力候補である。なぜこの分布が現れるのか、という議論はかなり興味深いが、今のところビシッとした答えはでない。
【つづき】
PR
| AKB48に見る順位分布 << | HOME | >> 最良の近似を求めて |
Calender
| 10 | 2025/11 | 12 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
Search in This Blog
Latest Comments
[03/30 川内のばば山田]
[03/30 川内のばば山田]
[08/06 Aterarie]
[07/05 Agazoger]
[07/01 Thomaskina]
Latest Posts
(11/16)
(04/28)
(04/16)
(04/11)
(04/05)
Latest Trackbacks
Category
Access Analysis

