2013/02/18 (Mon) 手筋？

KGS対局、互先の黒。左下△に切られたところ。ここで長考して・・・


下図１，３とやってみた。決まったら格好いい手筋。

隅を守るなら白４しかないが、中央下辺よりの白の一団が取れた。
黒11ではL2に打って生かし、右側の一団を取りに行くほうが最強だったかも。でもちょっと読みきれなかったので・・・。
中押し勝ち。

2013/02/17 (Sun) シチョウ

KGS対局、コミなしの黒。

黒１とハネ出して行ってみた。黒３にオシてなんとかなるだろう・・・。

白４から６にツグ手がないところまでは読めていた。白８に黒９のホウリコミ。


そこからシチョウ。
中押し勝ち。

2013/02/12 (Tue) 経済学：下級財・ギッフェン財を描く

TAとして、学部1年生にミクロ経済学を教えている。需要・供給曲線の話が終わり、そろそろ2財消費モデルが始まる。そこで、世界中どこでも教えるのが、財のタイプだ。

上級財 vs 下級財：この区別は、所得の上昇と共に需要量がどう変化するかに依存する。所得と同じ方向へ動くのが上級財（高級レストランでの食事）、所得と逆の方向へ動くのが下級財（ファーストフード）。

代替財 vs 補完財：これは、別の財の価格に対する需要量の反応による区別。財Aの価格が上がる時に、財Bの需要量が増えるなら代替財（ペプシに対するコカコーラ）、減るなら補完財（コーヒーに対する砂糖）。

ギッフェン財：非常に特殊な財で、財価格が上昇する時に需要量が上昇するものを言う。ギッフェン財を現実世界に見つけたらそれだけで大発見である（Jensen & MIller 2008 AER）。


財のタイプを解説する時には、無差別曲線グラフを用いる（なんかこういうやつ）。手描き（ペンタブなどを使って）で描くのは慣れればそう難しくはないのだけど、教える側としてはできればパソコンを使って描きたい。

そこで、いろんなタイプの無差別曲線を描くR関数を書いた（こちら）。
使い方は、
source("http://tips.futene.net/rsouko/utility.R")
normal() # 上級財
cross(.5) # 引数が０から１の間だと代替財
cross(-1) # 引数が０より小さいと補完財
inferior() # 下級財 
giffen() # ギッフェン財







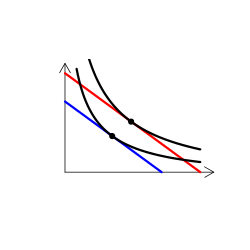
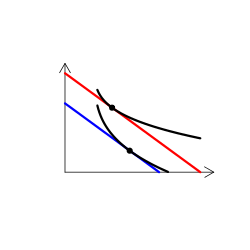
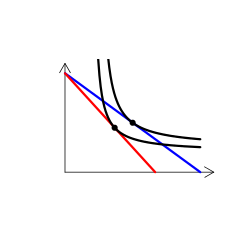
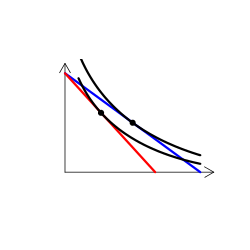
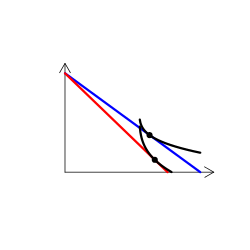
実は、これが意外に難しい。というのも、我々が普段良く用いる効用関数では、限られたタイプの需要構造しか表現できないからだ。

（１）コブ・ダグラス型効用関数 u(x,y) = a log(x) + b log(y)
最もポピュラーな効用関数だが、これを用いると2つの財はともに必ず上級財になり、かつ代替・補完の構造は生じない（つまり、財ｘの需要は財ｙの価格に依存しない）。

（２）CES効用関数 u(x,y) = (x^r + y^r)^(1/r), r <= 1
この関数の場合、2つの財はやはり上級財になる。rの値が0より大きければ代替財になり、rが0より小さければ補完財になる（r=0ならコブ・ダグラス型）。これを使えば、代替・補完関係を表現できる。

これら2つの効用関数では、下級財を表現することができない（ギッフェン財は下級財の特殊ケースなので同様）。実は思ったよりも根深い問題らしく、最近の研究論文で、非常にシンプルな効用関数が提案されている（Haagsma 2012 ISRN Economics）。

u(x, y) = a log(x-x0) - log(y0-y), 0 < a < 1.

この効用関数を用いると、
＊m - y0 < p x0 < m - a y0 の場合に内点解となり
＊財ｘは下級財
＊m > y0 なら財ｘはギッフェン財

となる。ただし、財ｙの価格を１に基準化して、ｍを所得、ｐを財ｘの価格としている。

この効用関数のミソは、財yについて凸関数になっている点（限界効用が逓増する）。したがって関数全体としては凹関数ではないのだけど、準凹ではあるので通常の無差別曲線を使った分析ができる。

2013/02/02 (Sat) 無勝負の新型

月刊碁ワールド2月号に、大橋5段による「無勝負の新型報告」という記事が掲載された。

こういう形らしい（黒番）。黒はP18のコウを取る一手。白はT19に抜くのがコウ立てで、黒はS18に打ち欠かなくてはいけない。




その結果が次図（白番）。続いて白P17に対して、今度は黒S19の2目取りがコウ立て。白はT18にウッテガエシに取る必要がある。すると前図に戻る。


循環系なので双方が妥協しない限り確かに無勝負だろうけど、これって長生とはどう違うのだろうか。

一般に知られている長生はこんな形（黒番）。
白C1に打たれると5目中手なので、黒C1に差し込む一手。その後、白E1、黒D1と2目を取り合う。


すると次の図になる（白番）。白はF1の眼取りしかないので、前図に戻る。


比較してみると、
大橋新型：「コウトリ→２目取り→ウチカキ→コウトリ→２目取り→ウチカキ」→反復
長生　　：「サシコミ→２目取り→２目取り→ウチカキ」→反復
周期は確かに違う。


実は、日本棋院規約でも長生ははっきりと定義されているわけではない（無勝負の例として載っているだけ）。手がかりを求めてWikipediaを繙くと、「コウ付き長生」なんて項目がある。

次図がそうらしい（黒番）。Wikiでは、黒A2のコウトリから循環するとされているけど、この形だけだと何もしなくても白は取られているのでちょっとピンとこない(すごく特別な形勢状況じゃないと駄目みたい)。
いずれにせよ、手順は黒A2, 白E1, 黒C1, 白A3, 黒B1, 白D1で一周するようだ。


で、比較。
大橋新型　　：「コウトリ→２目取り→ウチカキ→コウトリ→２目取り→ウチカキ」→反復
長生　　　　：「サシコミ→２目取り→２目取り→ウチカキ」→反復
コウ付き長生：「コウトリ→サシコミ→２目取り→コウトリ→サシコミ→２目取り」→反復

新型とちょっと似ているかも？


さらに、安倍吉輝９段の本では変わった長生の形が紹介されているらしい（ソース）。
こんな形。黒番で、今白がE18のコウを取ったところ。他にコウ材もないので、黒はA19にサシコミ、白は2目抜き、そこで黒はF18コウトリ。


すると下図のような形に（白番）。ここで白はD19にサシコミ、黒は2目を取り、白がコウを抜き返して元の図に戻る。

比較。
大橋新型　　：「コウトリ→２目取り→ウチカキ→コウトリ→２目取り→ウチカキ」→反復
長生　　　　：「サシコミ→２目取り→２目取り→ウチカキ」→反復
コウ付き長生：「コウトリ→サシコミ→２目取り→コウトリ→サシコミ→２目取り」→反復
安倍長生　　：「サシコミ→2目取り→コウトリ→サシコミ→2目取り→コウトリ」→反復

どうやら、コウ付き長生と安倍（9段の本に出てくる）長生は同じ流れのようだ（後者の方が断然良い例だが）。
大橋新型の特殊性は、用いられる傍コウが（サシコミによる）アテではなくて、眼持ちを睨んだ２目取りである点に認められるかもしれない。

名前を募集しているそうだけど、たぶん新種の長生ということで落ち着くんじゃないかな。長生大橋型、とか。

2013/02/02 (Sat) 駄目、詰まってますよ

KGS対局から。コミなしの黒。

今、白番。右辺の白はこれで死んでいると思っていたのだが。

白1から黒の駄目づまりを咎めて、仮に黒10という怪しい手が効いたとしても白生き。
久しぶりの大物を逃した。気を取り直して打って勝ち。