Yaleで、遊んで学ぶ日々。
Yaleで、遊んで学ぶ日々。
囲碁、ときどきプログラミング、ところにより経済。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
TAとして、学部1年生にミクロ経済学を教えている。需要・供給曲線の話が終わり、そろそろ2財消費モデルが始まる。そこで、世界中どこでも教えるのが、財のタイプだ。
上級財 vs 下級財:この区別は、所得の上昇と共に需要量がどう変化するかに依存する。所得と同じ方向へ動くのが上級財(高級レストランでの食事)、所得と逆の方向へ動くのが下級財(ファーストフード)。
代替財 vs 補完財:これは、別の財の価格に対する需要量の反応による区別。財Aの価格が上がる時に、財Bの需要量が増えるなら代替財(ペプシに対するコカコーラ)、減るなら補完財(コーヒーに対する砂糖)。
ギッフェン財:非常に特殊な財で、財価格が上昇する時に需要量が上昇するものを言う。ギッフェン財を現実世界に見つけたらそれだけで大発見である(Jensen & MIller 2008 AER)。
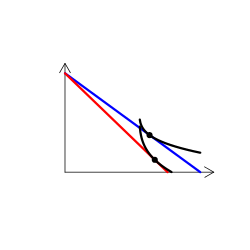
財のタイプを解説する時には、無差別曲線グラフを用いる(なんかこういうやつ)。手描き(ペンタブなどを使って)で描くのは慣れればそう難しくはないのだけど、教える側としてはできればパソコンを使って描きたい。
そこで、いろんなタイプの無差別曲線を描くR関数を書いた(こちら)。
使い方は、
source("http://tips.futene.net/rsouko/utility.R")
normal() # 上級財
cross(.5) # 引数が0から1の間だと代替財
cross(-1) # 引数が0より小さいと補完財
inferior() # 下級財
giffen() # ギッフェン財
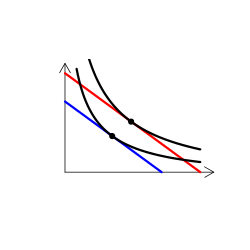
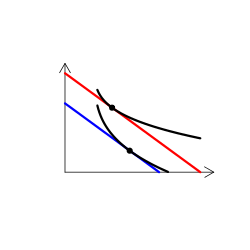
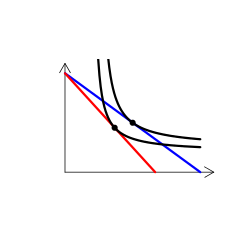
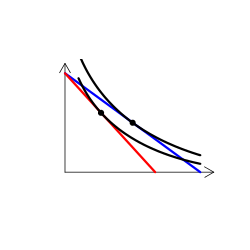
実は、これが意外に難しい。というのも、我々が普段良く用いる効用関数では、限られたタイプの需要構造しか表現できないからだ。
(1)コブ・ダグラス型効用関数 u(x,y) = a log(x) + b log(y)
最もポピュラーな効用関数だが、これを用いると2つの財はともに必ず上級財になり、かつ代替・補完の構造は生じない(つまり、財xの需要は財yの価格に依存しない)。
(2)CES効用関数 u(x,y) = (x^r + y^r)^(1/r), r <= 1
この関数の場合、2つの財はやはり上級財になる。rの値が0より大きければ代替財になり、rが0より小さければ補完財になる(r=0ならコブ・ダグラス型)。これを使えば、代替・補完関係を表現できる。
これら2つの効用関数では、下級財を表現することができない(ギッフェン財は下級財の特殊ケースなので同様)。実は思ったよりも根深い問題らしく、最近の研究論文で、非常にシンプルな効用関数が提案されている(Haagsma 2012 ISRN Economics)。
u(x, y) = a log(x-x0) - log(y0-y), 0 < a < 1.
この効用関数を用いると、
*m - y0 < p x0 < m - a y0 の場合に内点解となり
*財xは下級財
*m > y0 なら財xはギッフェン財
となる。ただし、財yの価格を1に基準化して、mを所得、pを財xの価格としている。
この効用関数のミソは、財yについて凸関数になっている点(限界効用が逓増する)。したがって関数全体としては凹関数ではないのだけど、準凹ではあるので通常の無差別曲線を使った分析ができる。
上級財 vs 下級財:この区別は、所得の上昇と共に需要量がどう変化するかに依存する。所得と同じ方向へ動くのが上級財(高級レストランでの食事)、所得と逆の方向へ動くのが下級財(ファーストフード)。
代替財 vs 補完財:これは、別の財の価格に対する需要量の反応による区別。財Aの価格が上がる時に、財Bの需要量が増えるなら代替財(ペプシに対するコカコーラ)、減るなら補完財(コーヒーに対する砂糖)。
ギッフェン財:非常に特殊な財で、財価格が上昇する時に需要量が上昇するものを言う。ギッフェン財を現実世界に見つけたらそれだけで大発見である(Jensen & MIller 2008 AER)。
財のタイプを解説する時には、無差別曲線グラフを用いる(なんかこういうやつ)。手描き(ペンタブなどを使って)で描くのは慣れればそう難しくはないのだけど、教える側としてはできればパソコンを使って描きたい。
そこで、いろんなタイプの無差別曲線を描くR関数を書いた(こちら)。
使い方は、
source("http://tips.futene.net/rsouko/utility.R")
normal() # 上級財
cross(.5) # 引数が0から1の間だと代替財
cross(-1) # 引数が0より小さいと補完財
inferior() # 下級財
giffen() # ギッフェン財
実は、これが意外に難しい。というのも、我々が普段良く用いる効用関数では、限られたタイプの需要構造しか表現できないからだ。
(1)コブ・ダグラス型効用関数 u(x,y) = a log(x) + b log(y)
最もポピュラーな効用関数だが、これを用いると2つの財はともに必ず上級財になり、かつ代替・補完の構造は生じない(つまり、財xの需要は財yの価格に依存しない)。
(2)CES効用関数 u(x,y) = (x^r + y^r)^(1/r), r <= 1
この関数の場合、2つの財はやはり上級財になる。rの値が0より大きければ代替財になり、rが0より小さければ補完財になる(r=0ならコブ・ダグラス型)。これを使えば、代替・補完関係を表現できる。
これら2つの効用関数では、下級財を表現することができない(ギッフェン財は下級財の特殊ケースなので同様)。実は思ったよりも根深い問題らしく、最近の研究論文で、非常にシンプルな効用関数が提案されている(Haagsma 2012 ISRN Economics)。
u(x, y) = a log(x-x0) - log(y0-y), 0 < a < 1.
この効用関数を用いると、
*m - y0 < p x0 < m - a y0 の場合に内点解となり
*財xは下級財
*m > y0 なら財xはギッフェン財
となる。ただし、財yの価格を1に基準化して、mを所得、pを財xの価格としている。
この効用関数のミソは、財yについて凸関数になっている点(限界効用が逓増する)。したがって関数全体としては凹関数ではないのだけど、準凹ではあるので通常の無差別曲線を使った分析ができる。
PR
Calender
| 11 | 2025/12 | 01 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
Search in This Blog
Latest Comments
[03/30 川内のばば山田]
[03/30 川内のばば山田]
[08/06 Aterarie]
[07/05 Agazoger]
[07/01 Thomaskina]
Latest Posts
(11/16)
(04/28)
(04/16)
(04/11)
(04/05)
Latest Trackbacks
Category
Access Analysis

