Yaleで、遊んで学ぶ日々。
Yaleで、遊んで学ぶ日々。
囲碁、ときどきプログラミング、ところにより経済。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
組み合わせ(n C k )を計算する時間は、nが大きくなるにつれて大きくなる。一番時間がかかるのはkがちょうどnの半分のところ(階乗の計算が大変)。逆にk=1またはk=nの時は、n C k = 1 なので簡単。
pythonでn C k を計算する関数としては、gmpy.comb() とscipy.misc.comb() の2つが有名どころらしい(参考URL)。このうち、gmpy.comb()は正確に組み合わせの数を計算するのに対して、scipy.misc.comb()のほうは、対数ガンマ関数を利用して近似値を返すらしい。そのため、後者のほうがスピードが速いとか。
実験してみたところ、次のような結果になった。
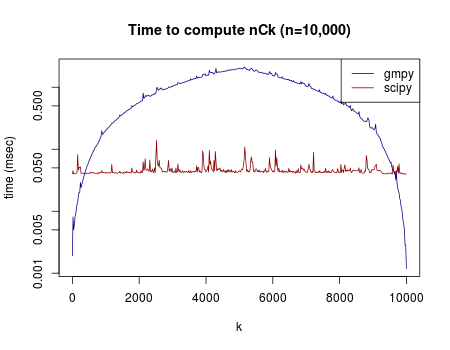
n = 10000を固定して、k の値を1から10000まで、色々変えて、それぞれの関数でn C k の計算にかかる時間を記録した。グラフのy軸は経過時間(ミリ秒)で。対数にしてある。
予想通り、gmpyのほうは階乗の計算が難しくなる中間のkについて、計算時間は長くなり、真ん中(k=5000)のあたりで最大になる。一方、近似値を計算するscipyの方は、そういった問題が起こらないらしく、一定の速度で計算できるらしい。そもそも計算の簡単な範囲(kが1に近いかnに近いか)では、gmpyで計算したほうが速いということもグラフから分かる。
使用したファイル:comb_test.py, comb-graph.R
pythonでn C k を計算する関数としては、gmpy.comb() とscipy.misc.comb() の2つが有名どころらしい(参考URL)。このうち、gmpy.comb()は正確に組み合わせの数を計算するのに対して、scipy.misc.comb()のほうは、対数ガンマ関数を利用して近似値を返すらしい。そのため、後者のほうがスピードが速いとか。
実験してみたところ、次のような結果になった。
n = 10000を固定して、k の値を1から10000まで、色々変えて、それぞれの関数でn C k の計算にかかる時間を記録した。グラフのy軸は経過時間(ミリ秒)で。対数にしてある。
予想通り、gmpyのほうは階乗の計算が難しくなる中間のkについて、計算時間は長くなり、真ん中(k=5000)のあたりで最大になる。一方、近似値を計算するscipyの方は、そういった問題が起こらないらしく、一定の速度で計算できるらしい。そもそも計算の簡単な範囲(kが1に近いかnに近いか)では、gmpyで計算したほうが速いということもグラフから分かる。
使用したファイル:comb_test.py, comb-graph.R
PR
| Latex: HTMLやワードに変換 << | HOME | >> 淡路先生の力戦2局 |
Calender
| 12 | 2026/01 | 02 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Search in This Blog
Latest Comments
[03/30 川内のばば山田]
[03/30 川内のばば山田]
[08/06 Aterarie]
[07/05 Agazoger]
[07/01 Thomaskina]
Latest Posts
(11/16)
(04/28)
(04/16)
(04/11)
(04/05)
Latest Trackbacks
Category
Access Analysis

