Yaleで、遊んで学ぶ日々。
Yaleで、遊んで学ぶ日々。
囲碁、ときどきプログラミング、ところにより経済。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
答え:攻め合いは黒良し。よって黒Bと打つべし! 黒は外駄目なしの花六で12手、白は外駄目9つの3目中手。3目中手は3手なので、合わせて12手。黒番なので手数が同じなら黒の勝ち。
中手は見た目以上に手数が長い。殺したと思ったら囲っている石の駄目が詰まって逆転負けなんてことになるとがっかりするので中手の手数は暗記しておくべきところ。
3目中手=3手
4目中手=5手
5目中手=8手
6目中手=12手
この背後には、漸化式があるというのが今日の話。
3目中手から考えよう。黒番から始まって白を取りきるまでに白は他に2手打てる。したがって3目中手は3手と分かる。
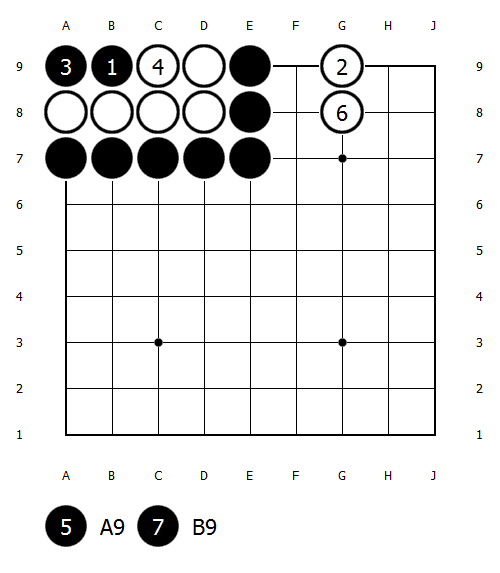
次に4目中手。手順は白6と白が3子抜いたところまで。ここまでで白は他に2手打てる。抜きあとは3目中手にほかならないから、ここからの手数は3手。したがって、手数は合計で2 + 3 = 5 と分かる。
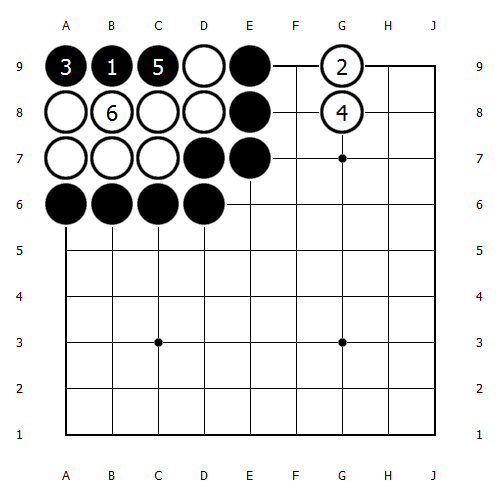
一般に、(n+1)目中手を n目中手にするには (n-1)手かかる。なぜnでなく n-1 なのかというと、一旦抜く手順があるためだ。したがって、a(n) をn目中手の手数とすれば、次の漸化式が導かれる。
a(n+1) = a(n) + (n-1)
a(3) = 3.
これを解くと、次のような一般式が得られる。
a(n) = [ (n-2)(n-1) + 4 ] / 2
・・・のだけど、まぁこれを覚えるくらいなら実際の数を覚えた方がいいか :P
ところで、1つ不思議なことがある。公式によると、a(2) = 2, a(1) = 2 なのだ。下図の左の形が2手なのは良いとして、右の形はどう考えても1手だ。なぜここにきて法則が破れるのか。
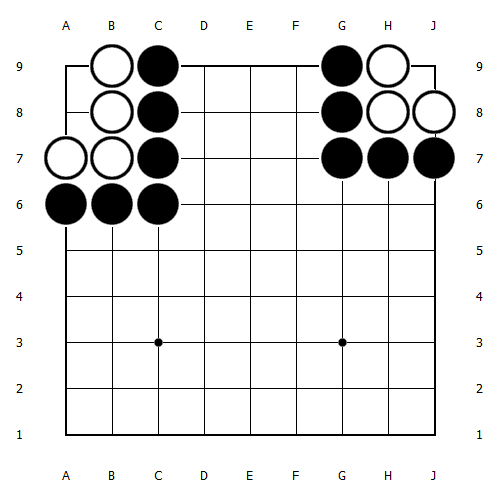
細かい話だが、理由は「一旦抜くかどうかの選択権が白にある」ためだろう。公式は、駄目が詰まったら一度抜くことを前提に作られている。4目中手以上なら、一度抜くことで手数を長引かせることができるからそれでいいが、3目中手の場合、抜いても抜かなくても手数は変わらない。それが2目以下になると、今度は抜いた瞬間に取られるから、抜かずに他へ打つ方が得になる。したがってこの公式は a(2) までにしか当てはまらない。無論、a(7) 以降は最悪でもセキになるのでそもそも攻め合いにならない。
中手は見た目以上に手数が長い。殺したと思ったら囲っている石の駄目が詰まって逆転負けなんてことになるとがっかりするので中手の手数は暗記しておくべきところ。
3目中手=3手
4目中手=5手
5目中手=8手
6目中手=12手
この背後には、漸化式があるというのが今日の話。
3目中手から考えよう。黒番から始まって白を取りきるまでに白は他に2手打てる。したがって3目中手は3手と分かる。
次に4目中手。手順は白6と白が3子抜いたところまで。ここまでで白は他に2手打てる。抜きあとは3目中手にほかならないから、ここからの手数は3手。したがって、手数は合計で2 + 3 = 5 と分かる。
一般に、(n+1)目中手を n目中手にするには (n-1)手かかる。なぜnでなく n-1 なのかというと、一旦抜く手順があるためだ。したがって、a(n) をn目中手の手数とすれば、次の漸化式が導かれる。
a(n+1) = a(n) + (n-1)
a(3) = 3.
これを解くと、次のような一般式が得られる。
a(n) = [ (n-2)(n-1) + 4 ] / 2
・・・のだけど、まぁこれを覚えるくらいなら実際の数を覚えた方がいいか :P
ところで、1つ不思議なことがある。公式によると、a(2) = 2, a(1) = 2 なのだ。下図の左の形が2手なのは良いとして、右の形はどう考えても1手だ。なぜここにきて法則が破れるのか。
細かい話だが、理由は「一旦抜くかどうかの選択権が白にある」ためだろう。公式は、駄目が詰まったら一度抜くことを前提に作られている。4目中手以上なら、一度抜くことで手数を長引かせることができるからそれでいいが、3目中手の場合、抜いても抜かなくても手数は変わらない。それが2目以下になると、今度は抜いた瞬間に取られるから、抜かずに他へ打つ方が得になる。したがってこの公式は a(2) までにしか当てはまらない。無論、a(7) 以降は最悪でもセキになるのでそもそも攻め合いにならない。
PR
Calender
| 08 | 2025/09 | 10 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 |
Search in This Blog
Latest Comments
[03/30 川内のばば山田]
[03/30 川内のばば山田]
[08/06 Aterarie]
[07/05 Agazoger]
[07/01 Thomaskina]
Latest Posts
(11/16)
(04/28)
(04/16)
(04/11)
(04/05)
Latest Trackbacks
Category
Access Analysis

