Yaleで、遊んで学ぶ日々。
Yaleで、遊んで学ぶ日々。
囲碁、ときどきプログラミング、ところにより経済。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
TAとして、学部1年生にミクロ経済学を教えている。需要・供給曲線の話が終わり、そろそろ2財消費モデルが始まる。そこで、世界中どこでも教えるのが、財のタイプだ。
上級財 vs 下級財:この区別は、所得の上昇と共に需要量がどう変化するかに依存する。所得と同じ方向へ動くのが上級財(高級レストランでの食事)、所得と逆の方向へ動くのが下級財(ファーストフード)。
代替財 vs 補完財:これは、別の財の価格に対する需要量の反応による区別。財Aの価格が上がる時に、財Bの需要量が増えるなら代替財(ペプシに対するコカコーラ)、減るなら補完財(コーヒーに対する砂糖)。
ギッフェン財:非常に特殊な財で、財価格が上昇する時に需要量が上昇するものを言う。ギッフェン財を現実世界に見つけたらそれだけで大発見である(Jensen & MIller 2008 AER)。
財のタイプを解説する時には、無差別曲線グラフを用いる(なんかこういうやつ)。手描き(ペンタブなどを使って)で描くのは慣れればそう難しくはないのだけど、教える側としてはできればパソコンを使って描きたい。
そこで、いろんなタイプの無差別曲線を描くR関数を書いた(こちら)。
使い方は、
source("http://tips.futene.net/rsouko/utility.R")
normal() # 上級財
cross(.5) # 引数が0から1の間だと代替財
cross(-1) # 引数が0より小さいと補完財
inferior() # 下級財
giffen() # ギッフェン財
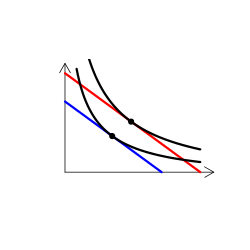
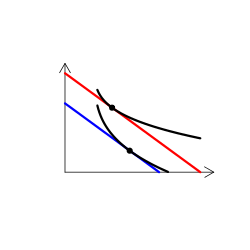
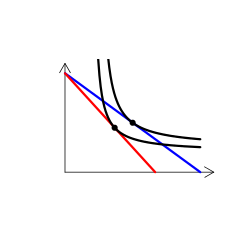
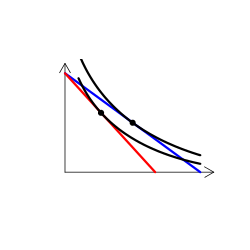
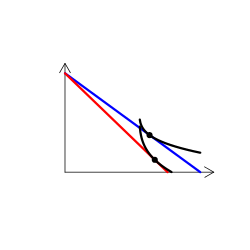
実は、これが意外に難しい。というのも、我々が普段良く用いる効用関数では、限られたタイプの需要構造しか表現できないからだ。
(1)コブ・ダグラス型効用関数 u(x,y) = a log(x) + b log(y)
最もポピュラーな効用関数だが、これを用いると2つの財はともに必ず上級財になり、かつ代替・補完の構造は生じない(つまり、財xの需要は財yの価格に依存しない)。
(2)CES効用関数 u(x,y) = (x^r + y^r)^(1/r), r <= 1
この関数の場合、2つの財はやはり上級財になる。rの値が0より大きければ代替財になり、rが0より小さければ補完財になる(r=0ならコブ・ダグラス型)。これを使えば、代替・補完関係を表現できる。
これら2つの効用関数では、下級財を表現することができない(ギッフェン財は下級財の特殊ケースなので同様)。実は思ったよりも根深い問題らしく、最近の研究論文で、非常にシンプルな効用関数が提案されている(Haagsma 2012 ISRN Economics)。
u(x, y) = a log(x-x0) - log(y0-y), 0 < a < 1.
この効用関数を用いると、
*m - y0 < p x0 < m - a y0 の場合に内点解となり
*財xは下級財
*m > y0 なら財xはギッフェン財
となる。ただし、財yの価格を1に基準化して、mを所得、pを財xの価格としている。
この効用関数のミソは、財yについて凸関数になっている点(限界効用が逓増する)。したがって関数全体としては凹関数ではないのだけど、準凹ではあるので通常の無差別曲線を使った分析ができる。
上級財 vs 下級財:この区別は、所得の上昇と共に需要量がどう変化するかに依存する。所得と同じ方向へ動くのが上級財(高級レストランでの食事)、所得と逆の方向へ動くのが下級財(ファーストフード)。
代替財 vs 補完財:これは、別の財の価格に対する需要量の反応による区別。財Aの価格が上がる時に、財Bの需要量が増えるなら代替財(ペプシに対するコカコーラ)、減るなら補完財(コーヒーに対する砂糖)。
ギッフェン財:非常に特殊な財で、財価格が上昇する時に需要量が上昇するものを言う。ギッフェン財を現実世界に見つけたらそれだけで大発見である(Jensen & MIller 2008 AER)。
財のタイプを解説する時には、無差別曲線グラフを用いる(なんかこういうやつ)。手描き(ペンタブなどを使って)で描くのは慣れればそう難しくはないのだけど、教える側としてはできればパソコンを使って描きたい。
そこで、いろんなタイプの無差別曲線を描くR関数を書いた(こちら)。
使い方は、
source("http://tips.futene.net/rsouko/utility.R")
normal() # 上級財
cross(.5) # 引数が0から1の間だと代替財
cross(-1) # 引数が0より小さいと補完財
inferior() # 下級財
giffen() # ギッフェン財
実は、これが意外に難しい。というのも、我々が普段良く用いる効用関数では、限られたタイプの需要構造しか表現できないからだ。
(1)コブ・ダグラス型効用関数 u(x,y) = a log(x) + b log(y)
最もポピュラーな効用関数だが、これを用いると2つの財はともに必ず上級財になり、かつ代替・補完の構造は生じない(つまり、財xの需要は財yの価格に依存しない)。
(2)CES効用関数 u(x,y) = (x^r + y^r)^(1/r), r <= 1
この関数の場合、2つの財はやはり上級財になる。rの値が0より大きければ代替財になり、rが0より小さければ補完財になる(r=0ならコブ・ダグラス型)。これを使えば、代替・補完関係を表現できる。
これら2つの効用関数では、下級財を表現することができない(ギッフェン財は下級財の特殊ケースなので同様)。実は思ったよりも根深い問題らしく、最近の研究論文で、非常にシンプルな効用関数が提案されている(Haagsma 2012 ISRN Economics)。
u(x, y) = a log(x-x0) - log(y0-y), 0 < a < 1.
この効用関数を用いると、
*m - y0 < p x0 < m - a y0 の場合に内点解となり
*財xは下級財
*m > y0 なら財xはギッフェン財
となる。ただし、財yの価格を1に基準化して、mを所得、pを財xの価格としている。
この効用関数のミソは、財yについて凸関数になっている点(限界効用が逓増する)。したがって関数全体としては凹関数ではないのだけど、準凹ではあるので通常の無差別曲線を使った分析ができる。
PR
詳しい資料が↓のURLに出ていた。昨年末の日付になっているが、おそらくほとんど同じデータを使っていると思う。
そもそも相対的貧困率というのは、可処分所得の中央値の半分未満の比率であるので、本質的に不平等指標だ。同じ人物でも比べる対象が違えば貧困になったりなくなったりする(正確には、可処分所得は世帯所得の個人割合等価という指標(世帯所得÷世帯人数の平方根)で計られる)。例えば、20ー64歳女性の枠では貧困と判定された人が、20代の中では貧困ではないことがありえる。あくまで「相対的に」なのだ。ということは、同程度の所得水準であるべき枠の中で比べなくては意味がない。極論、外資系投資銀行に勤める人51人とフリーター49人で構成されるグループで計れば、おそらく相対的貧困率は49%くらいになるけど、だからって深刻ですねえとはならない。グループの決め方が大事なのだ。
見出しに出ている、「20ー64歳単身女性の貧困率」については、年齢層の幅広さが気になる。つまり、この貧困率は、世代間の所得の差を反映している可能性がある。しかし、20代より40代の方が高所得なのは自然なことで、それ自体は悪いことではない。だって、その20代の人たちはいずれ40代になるわけだから。
そういうわけで年齢別の貧困率を見てみると、20ー64歳女性はどの層も15%くらいで推移している。やはり、記事にあった「32%」は、世代間格差を捉えたに過ぎないのだろうか。
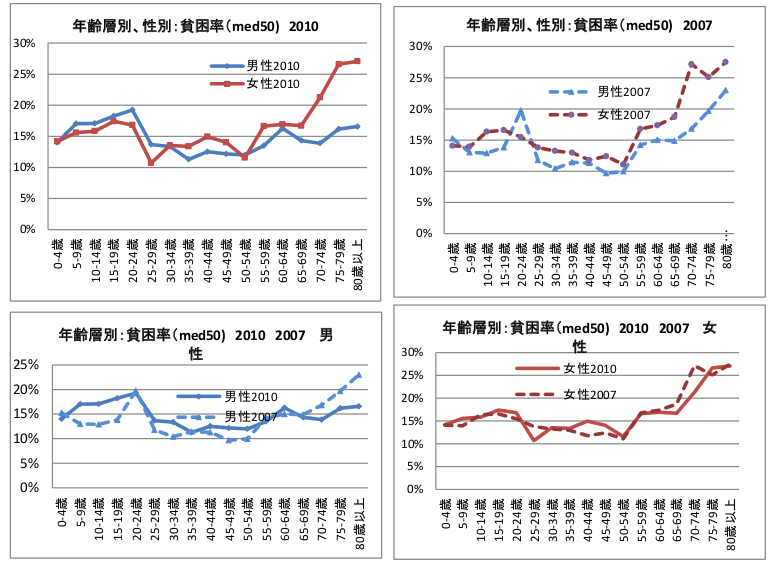
結論を出すのはまだ早い。もう少し考えてみる。上のグラフは、単に年齢別であって単身に限定していない。単身者に特有の問題がある可能性は拭いきれない。しかし、残念ながら。年齢別かつ世帯構成別の貧困率はデータに出ていないから直接は検証できない。ただ、注目すべきことに、「20ー64歳夫婦のみ世帯」の貧困率は約10%と低いのだ。
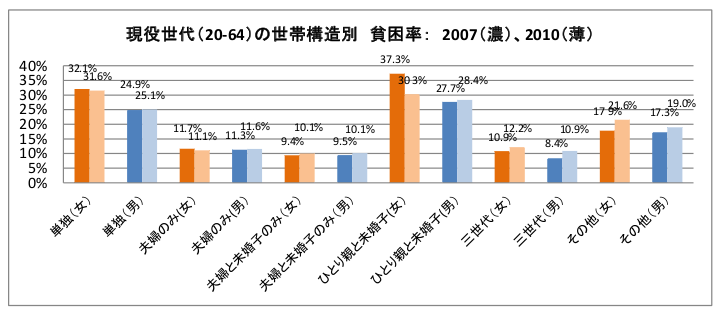
むむ、やはりこれは単身者に特有の貧困問題があるのだろうか。一つの可能性は、世帯の種類によって年齢構成比が違う、ということがある。そこで、同じ研究所が公開しているデータを見てみる→リンク。下の表は、世帯の種類別・年齢別で世帯数を比べている。単身者は若年層の割合が相対的に高いから、所得の低い年代が多いと言えるかもしれない。一方、夫婦のみに関しては、50代以降の年齢の高い層が多くて、こちらは所得の高い層が多いかもしれない。眺めてみてもよくわからんなー。
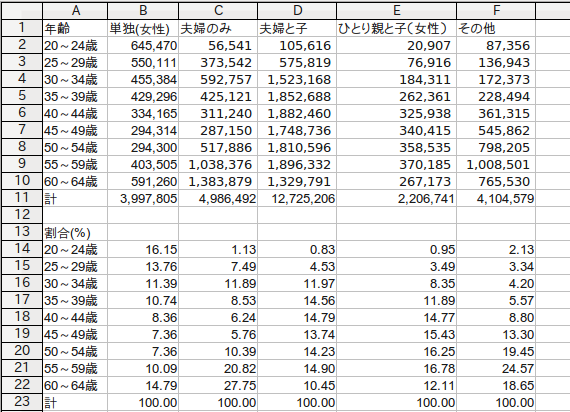
多少経済学者っぽい物言いをすれば...
「キャリアウーマンほど売れ残る」→「40代単身女性は高所得」とか、
「夫婦のみ家庭では、旦那の稼ぎが少ないと共働きにするが、十分大きいと妻が家庭に入る→1人分の可処分所得は年齢を重ねてもあまり増えない」
とか、色々言うことはできて、理由をつけて記事を批判したくなるのだけど、ちょっとデータ不足で何とも言えないかな。単身層に独特の問題がないとも言えないが、あるとも言えない。
ただ、少なくとも若年単身女性の貧困率は、そんなに高くないだろうと想像する。なぜなら、この年齢層の貧困率は大体15%くらいで、その半分以上は単身だからだ。もし単身層の貧困率が高いなら、全体の貧困率も大きくでそうなものだと思うのだが、どうだろうか。
ところで、数字そのものは、昨年12月の時点ですでに出ているのに、今になって「わかった」という記事がでるのはどういうことなんだろう。報道のタイミングを見計らっていたのか、それとも?
結論を出すのはまだ早い。もう少し考えてみる。上のグラフは、単に年齢別であって単身に限定していない。単身者に特有の問題がある可能性は拭いきれない。しかし、残念ながら。年齢別かつ世帯構成別の貧困率はデータに出ていないから直接は検証できない。ただ、注目すべきことに、「20ー64歳夫婦のみ世帯」の貧困率は約10%と低いのだ。
むむ、やはりこれは単身者に特有の貧困問題があるのだろうか。一つの可能性は、世帯の種類によって年齢構成比が違う、ということがある。そこで、同じ研究所が公開しているデータを見てみる→リンク。下の表は、世帯の種類別・年齢別で世帯数を比べている。単身者は若年層の割合が相対的に高いから、所得の低い年代が多いと言えるかもしれない。一方、夫婦のみに関しては、50代以降の年齢の高い層が多くて、こちらは所得の高い層が多いかもしれない。眺めてみてもよくわからんなー。
多少経済学者っぽい物言いをすれば...
「キャリアウーマンほど売れ残る」→「40代単身女性は高所得」とか、
「夫婦のみ家庭では、旦那の稼ぎが少ないと共働きにするが、十分大きいと妻が家庭に入る→1人分の可処分所得は年齢を重ねてもあまり増えない」
とか、色々言うことはできて、理由をつけて記事を批判したくなるのだけど、ちょっとデータ不足で何とも言えないかな。単身層に独特の問題がないとも言えないが、あるとも言えない。
ただ、少なくとも若年単身女性の貧困率は、そんなに高くないだろうと想像する。なぜなら、この年齢層の貧困率は大体15%くらいで、その半分以上は単身だからだ。もし単身層の貧困率が高いなら、全体の貧困率も大きくでそうなものだと思うのだが、どうだろうか。
ところで、数字そのものは、昨年12月の時点ですでに出ているのに、今になって「わかった」という記事がでるのはどういうことなんだろう。報道のタイミングを見計らっていたのか、それとも?
Starting from an arbitrary point, draw a line of a certain length, then turn 36 degree, draw a line of the same length, turn 36 degree, draw a line of the same length,...
Repeating this process five times brings you back to the original point.
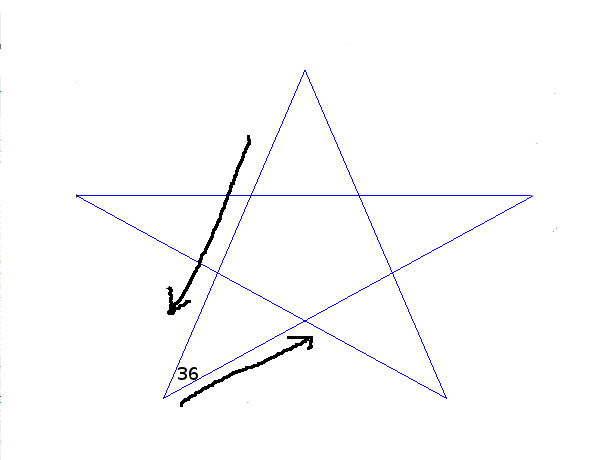
Question: Find a general condition for an angle θ to come back to the original point. Given such θ, how many times do you need to repeat the process until you are back?
Repeating this process five times brings you back to the original point.
Question: Find a general condition for an angle θ to come back to the original point. Given such θ, how many times do you need to repeat the process until you are back?
【前回】
【年齢調整死亡率, 標準化死亡比:人口構成を調整する】
粗死亡率の弱点は、人口構成が異なる場合の比較が難しいところにある。そこで考え出されたのが年齢調整死亡率 (direct age-adjusted mortality rate, DAR) だ。DARは次のように定義される。
DAR(i) = Σ_k [ d(i,k) / n(i,k) ] * R(k)
k: 年齢グループ
d(i,k): 地域iにおけるグループkの死亡数
n(i,k):地域iにおけるグループkの人口
R(k): 標準人口構成におけるグループkの割合
式は多少複雑だが、理屈はシンプルだ。まず、グループごとに死亡率を求める。DARは、「そのグループ別死亡率のもとで、仮に標準的な人口構成だったとした場合」の死亡率だ。だから、人口構成が標準人口構成と同一である場合(つまり n(i,k) / n(i) = R(k) )には、DARとCMRは一致する。
標準人口は何でも良い。厚生労働省では、今のところ昭和60年のモデル人口が用いられているようだ(→厚生労働省:年齢調整死亡率について)。
また、一般には年齢構成について調整されることが多いが、実際には人口をグルーピングする方法は何でも良い。性別や職業・産業構成などで調整するのも時に有用だろう。
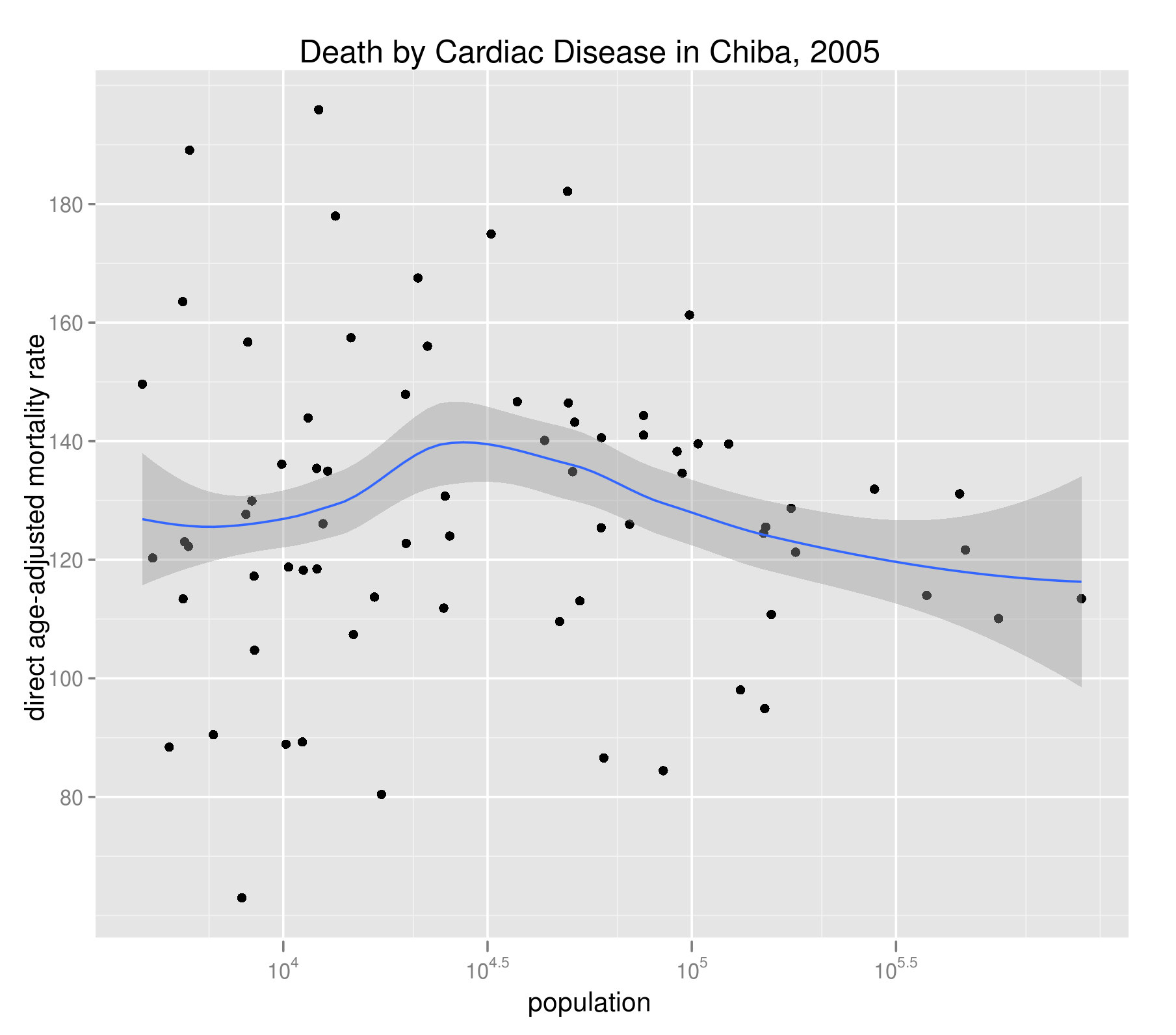
下図では、千葉県の心疾患(高血圧性を除く)による死亡について、性・年齢5歳階級グループで調整した各市町村のDARを人口とプロットしている。標準人口には、同年の千葉県全体の人口構成を用いた。CMRに見られたような負の相関が消えている。間接的ではあるが、CMRと人口規模の負の相関が人口構成を介する擬似相関であることを示唆している。
DARの1つの弱点は、詳細な死亡データが必要となる点である。グループ別の死亡者数(数式でのd(i,k))は、細かすぎて手に入らないことも多い。この点をカバーする代替指標の1つが、標準化死亡比(standardized mortality rate, SMR)だ。
SMR(i) = d(i) / Σ_k [ n(i,k) * P(k) ]
P(k): 標準的なグループkの死亡率
定義の分母は、標準的なグループkの死亡率と地域iの人口構成から計算される「予想死亡者数」となっており、SMRはその「予想死亡者数」が実際の死亡者数からどれだけ乖離しているかを表す指標だ。一般には、さらに100倍して100を基準とすることも多い。
SMRの1つの問題は、P(k)をどう定義するかだが、これには地域iの属する上位地域の死亡率を用いることが多い。例えば千葉県の市町村のSMRを計算する時には、千葉県全体の死亡率を用いるのが一案である。各都道府県のSMRの算出には日本全国の、各国のSMRの算出には世界全体の死亡率、といった具合だ。
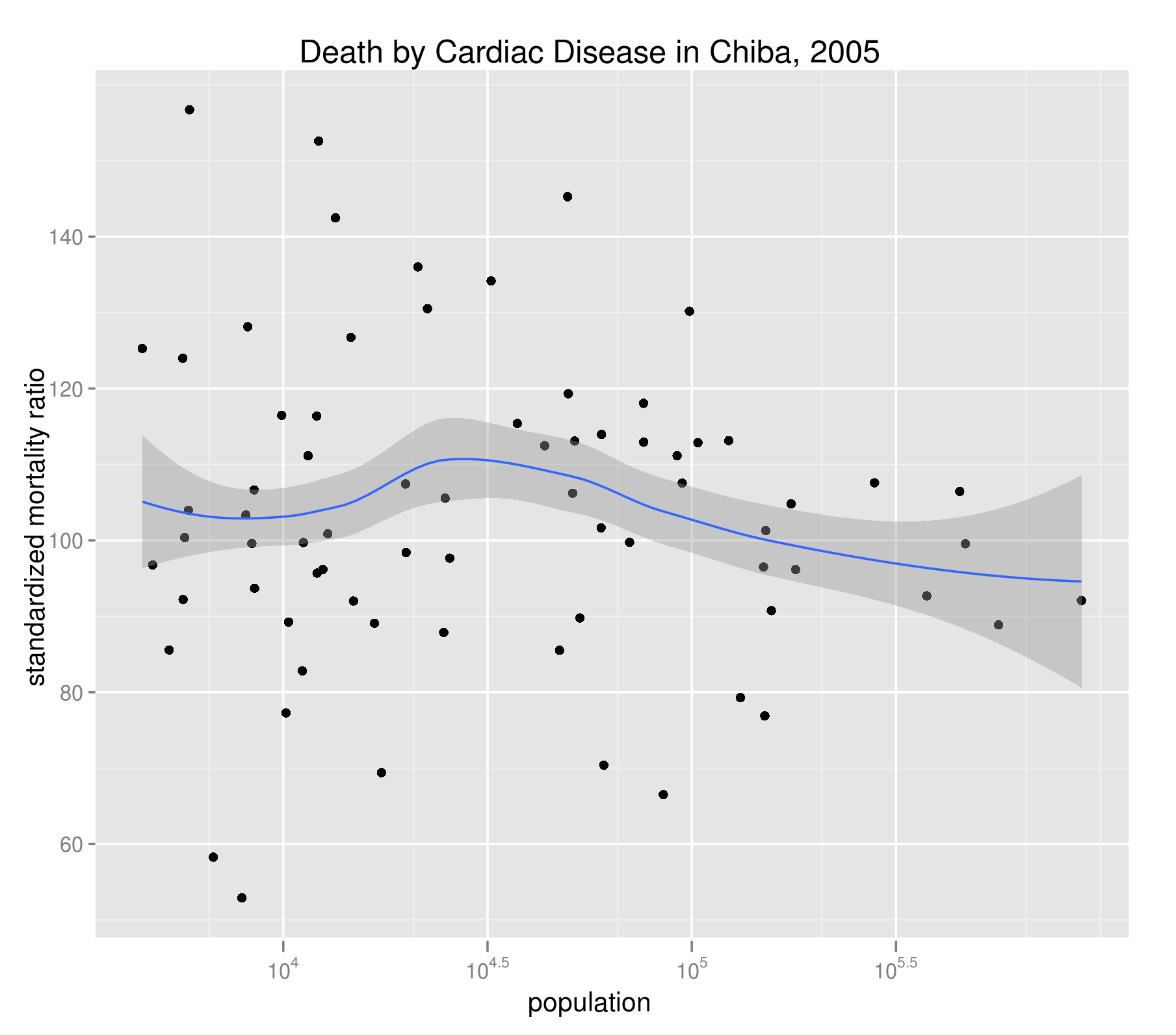
下図には、千葉県内の各市町村の心疾患(高血圧性を除く)に関するSMRとその人口の散布図を示した。グループ分けは、同じく性・年齢5歳階級で行っている。DARとよく似ており、人口構成による擬似相関はきっちり排除できている。
SMRの計算に必要な死亡データは地域別の総死亡数(d(i))だけなので、DARに比べてデータ面での要請は緩い。一方、その挙動はDARに近いのでなかなか優秀な指標のようだ。
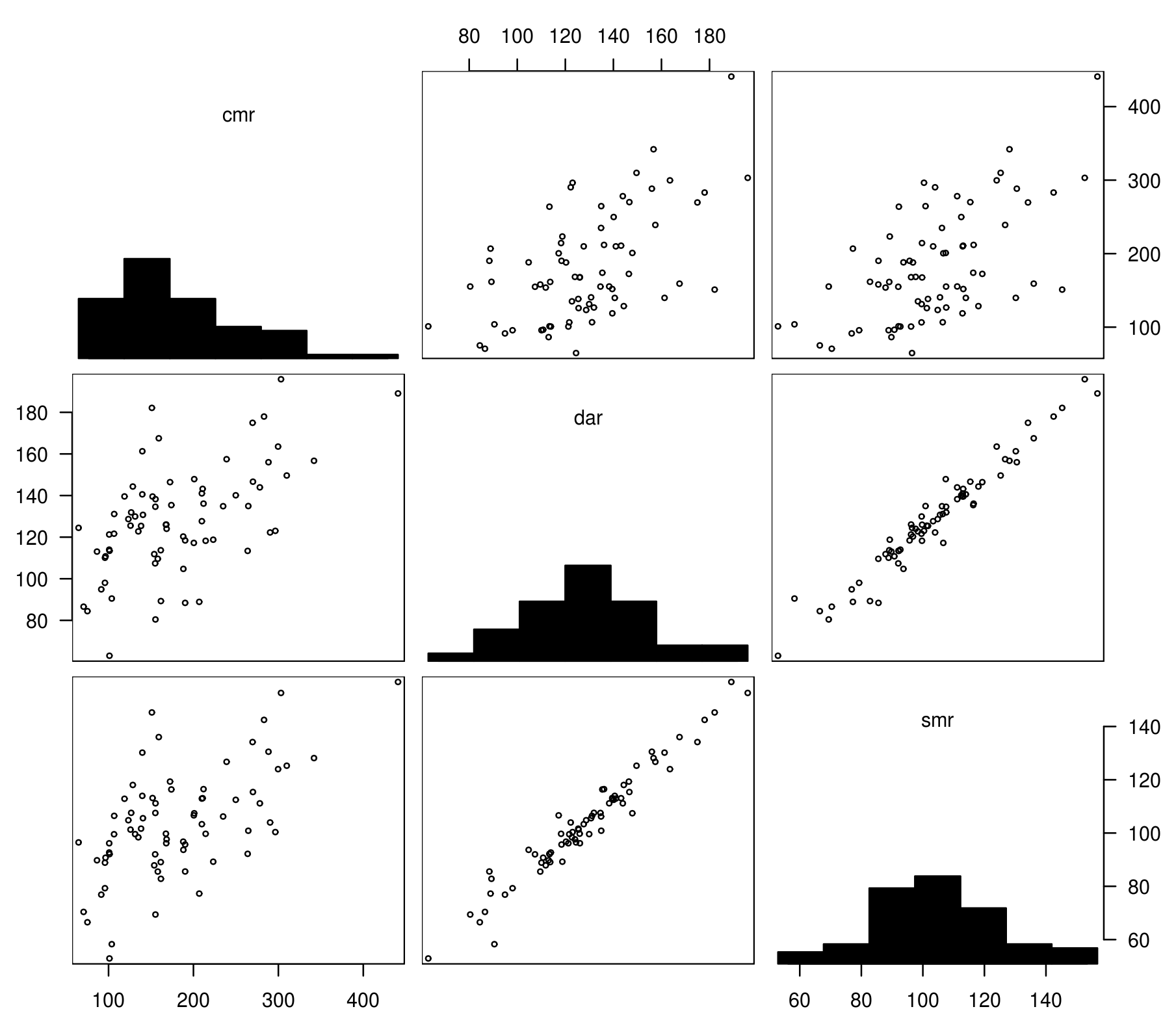
下図では、粗死亡率 (CMR), 年齢調整死亡率 (DAR), 標準化死亡比 (SMR) の3指標の関係を散布図に表した。DARとSMFの線形相関が極めて強く、一方CMRは他の指標とそこそこの相関を持つにすぎないことが分かる。
さて、死亡指標の比較には、年齢調整死亡率 (DAR) と 標準化死亡比 (SMR) の2つが非常によく用いられるが、それでも弱点がないわけではない。両指標の1つの弱点は、小地域における不安定性である。
先のグラフからも見て分かる通り、DARもSMRも、人口が小さくなるにつれて上下の振れ幅が大きくなっている(CMRも同様)。心疾患(高血圧性を除く)は比較的頻度の高い死因なので、一般には小規模地域における不安定性はもっと深刻になりうる。
端的に言えば、不安定性の原因はデータ不足にある。人口規模の小さい地域においては大数の法則が十分に成立しないため、死亡率が収束しきらないわけである。そこで、データ不足を補う方法を次に考える。
【つづき】
【年齢調整死亡率, 標準化死亡比:人口構成を調整する】
粗死亡率の弱点は、人口構成が異なる場合の比較が難しいところにある。そこで考え出されたのが年齢調整死亡率 (direct age-adjusted mortality rate, DAR) だ。DARは次のように定義される。
DAR(i) = Σ_k [ d(i,k) / n(i,k) ] * R(k)
k: 年齢グループ
d(i,k): 地域iにおけるグループkの死亡数
n(i,k):地域iにおけるグループkの人口
R(k): 標準人口構成におけるグループkの割合
式は多少複雑だが、理屈はシンプルだ。まず、グループごとに死亡率を求める。DARは、「そのグループ別死亡率のもとで、仮に標準的な人口構成だったとした場合」の死亡率だ。だから、人口構成が標準人口構成と同一である場合(つまり n(i,k) / n(i) = R(k) )には、DARとCMRは一致する。
標準人口は何でも良い。厚生労働省では、今のところ昭和60年のモデル人口が用いられているようだ(→厚生労働省:年齢調整死亡率について)。
また、一般には年齢構成について調整されることが多いが、実際には人口をグルーピングする方法は何でも良い。性別や職業・産業構成などで調整するのも時に有用だろう。
下図では、千葉県の心疾患(高血圧性を除く)による死亡について、性・年齢5歳階級グループで調整した各市町村のDARを人口とプロットしている。標準人口には、同年の千葉県全体の人口構成を用いた。CMRに見られたような負の相関が消えている。間接的ではあるが、CMRと人口規模の負の相関が人口構成を介する擬似相関であることを示唆している。
DARの1つの弱点は、詳細な死亡データが必要となる点である。グループ別の死亡者数(数式でのd(i,k))は、細かすぎて手に入らないことも多い。この点をカバーする代替指標の1つが、標準化死亡比(standardized mortality rate, SMR)だ。
SMR(i) = d(i) / Σ_k [ n(i,k) * P(k) ]
P(k): 標準的なグループkの死亡率
定義の分母は、標準的なグループkの死亡率と地域iの人口構成から計算される「予想死亡者数」となっており、SMRはその「予想死亡者数」が実際の死亡者数からどれだけ乖離しているかを表す指標だ。一般には、さらに100倍して100を基準とすることも多い。
SMRの1つの問題は、P(k)をどう定義するかだが、これには地域iの属する上位地域の死亡率を用いることが多い。例えば千葉県の市町村のSMRを計算する時には、千葉県全体の死亡率を用いるのが一案である。各都道府県のSMRの算出には日本全国の、各国のSMRの算出には世界全体の死亡率、といった具合だ。
下図には、千葉県内の各市町村の心疾患(高血圧性を除く)に関するSMRとその人口の散布図を示した。グループ分けは、同じく性・年齢5歳階級で行っている。DARとよく似ており、人口構成による擬似相関はきっちり排除できている。
SMRの計算に必要な死亡データは地域別の総死亡数(d(i))だけなので、DARに比べてデータ面での要請は緩い。一方、その挙動はDARに近いのでなかなか優秀な指標のようだ。
下図では、粗死亡率 (CMR), 年齢調整死亡率 (DAR), 標準化死亡比 (SMR) の3指標の関係を散布図に表した。DARとSMFの線形相関が極めて強く、一方CMRは他の指標とそこそこの相関を持つにすぎないことが分かる。
さて、死亡指標の比較には、年齢調整死亡率 (DAR) と 標準化死亡比 (SMR) の2つが非常によく用いられるが、それでも弱点がないわけではない。両指標の1つの弱点は、小地域における不安定性である。
先のグラフからも見て分かる通り、DARもSMRも、人口が小さくなるにつれて上下の振れ幅が大きくなっている(CMRも同様)。心疾患(高血圧性を除く)は比較的頻度の高い死因なので、一般には小規模地域における不安定性はもっと深刻になりうる。
端的に言えば、不安定性の原因はデータ不足にある。人口規模の小さい地域においては大数の法則が十分に成立しないため、死亡率が収束しきらないわけである。そこで、データ不足を補う方法を次に考える。
【つづき】
Calender
| 12 | 2026/01 | 02 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Search in This Blog
Latest Comments
[03/30 川内のばば山田]
[03/30 川内のばば山田]
[08/06 Aterarie]
[07/05 Agazoger]
[07/01 Thomaskina]
Latest Posts
(11/16)
(04/28)
(04/16)
(04/11)
(04/05)
Latest Trackbacks
Category
Access Analysis


