Yaleで、遊んで学ぶ日々。
Yaleで、遊んで学ぶ日々。
囲碁、ときどきプログラミング、ところにより経済。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
分野を問わず、死亡データを扱う場面は多い。公衆衛生学では、伝染病による死亡率が重要な関心事項の1つであるし、開発学においては乳幼児死亡率が国の発展のバロメータの1つとみなされる。都市計画では交通事故死の頻度を議論することもあるだろうし、自殺率や殺人死亡率は100年前から社会学の中心テーマだ。
死亡データの比較には、様々な死亡指標が用いられる。単純に死亡者数を人口で割ったいわゆる死亡率から、数値計算を行わなければ計算できないような複雑なものまで多種多様である。それらの死亡指標を具体的に計算しながら勉強しよう、というのがこの記事の目的。
【データ】
ネット上を検索したところ、千葉県の死亡データが市町村レベルで細かく手に入ったので、これを使用する。今回は平成17年の市町村別・死因別・性別・年齢階級別の死亡数を選んだ(→ソース)。平成17年にしたのは、国勢調査年なので後々便利かと思っただけで、深い理由はない。対応する人口データには、「住民基本台帳に基づく人口、人口動態及び世帯数調査」を用いた。市町村別・性別・年齢階級別の人口の年次データがe-statで手に入る(トップページから、「政府統計全体から探す」 >> 統計分野別「人口・世帯」 >> 「住民基本台帳に基づく人口、人口動態及び世帯数調査」 )。平成17年中の市町村合併を反映して、両データをマッチングする際には、夷隅町・大原町・岬町の3つをいすみ市に、干潟町・海上町・飯岡町の3つを旭市に計上した(→合併情報)。
【粗死亡率:人口規模を調整する】
死亡データを比較する時、死者数そのものを比べることにはほとんどの場合に意味がない。母数人口の規模が通常一定ではないからだ。言うまでもなく、人が多くいればそれだけ多くの死者が出やすいのだから、人口の差を加味しない比較はアンフェアである。
人口規模の違いを調整するために、死者数を母数人口で割ったものを「粗死亡率 (crude mortality rate, CMR)」と呼ぶ。小数点以下にゼロが並ぶと格好悪いので、10万をかけて「人口10万人あたり死亡者数」として計算するのが一般的。
CMR(i) = d(i) / n(i)
i: 地域
d(i): 地域iの死亡数
n(i): 地域iの人口
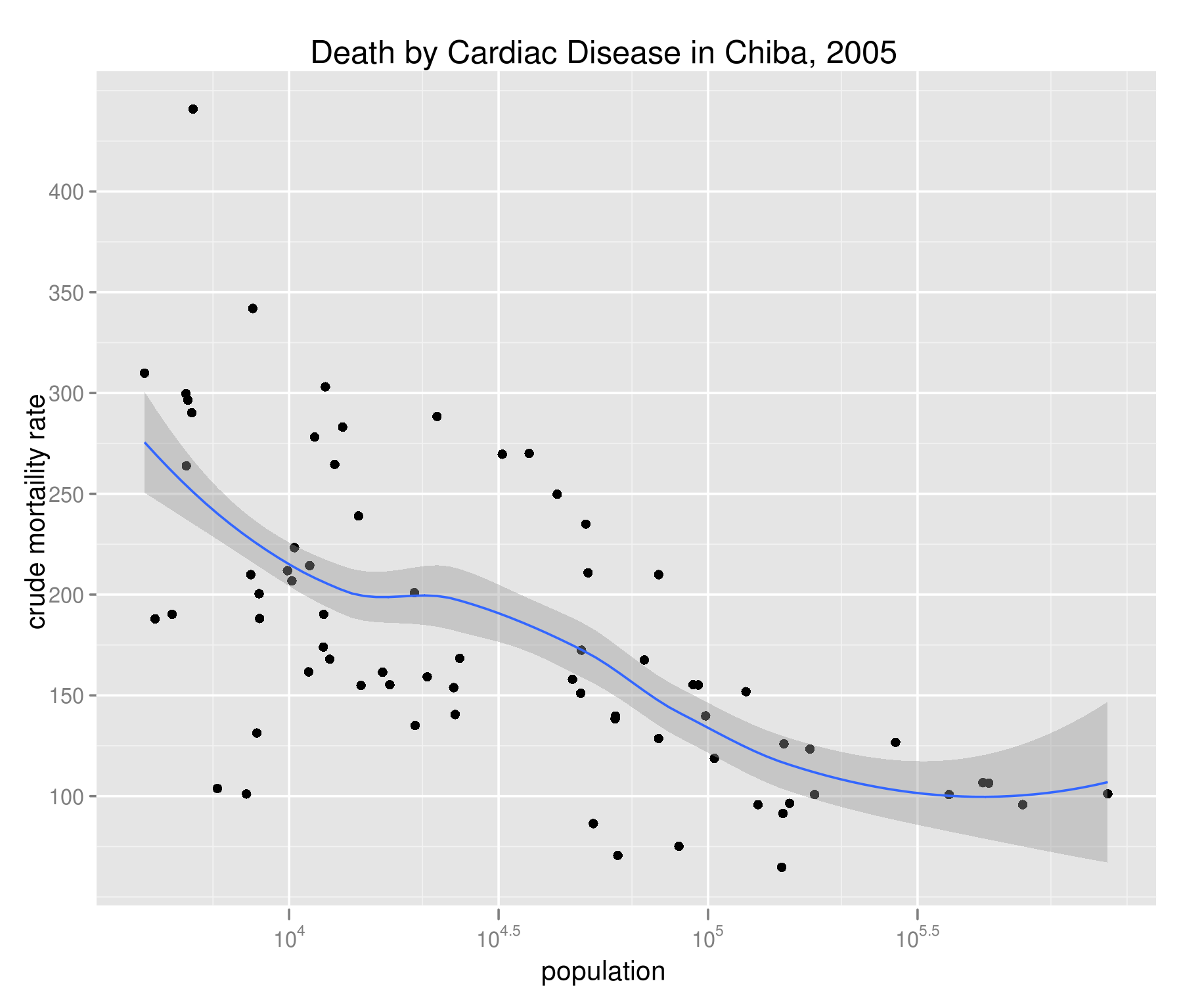
下図は、千葉県の各市町村について、心疾患(高血圧性を除く)による粗死亡率を求め、人口との散布図を描いたもの。強い負の相関が確認できる。なぜ負の相関なのか?
「人口規模が小さくなると心疾患のリスクが高まる」、と考えるのは早合点。これは典型的な擬似相関と見るべきだ。つまり、人口の小さいところは相対的に田舎で、高齢者の割合が大きく、そのため心疾患による死亡率が高くなるというわけだ。そういうわけで、千葉市と三芳村を比べるには、粗死亡率ではまだ不適格ということになる。人口規模の次は、人口構成の違いを調整する必要がある。
【つづき】
死亡データの比較には、様々な死亡指標が用いられる。単純に死亡者数を人口で割ったいわゆる死亡率から、数値計算を行わなければ計算できないような複雑なものまで多種多様である。それらの死亡指標を具体的に計算しながら勉強しよう、というのがこの記事の目的。
【データ】
ネット上を検索したところ、千葉県の死亡データが市町村レベルで細かく手に入ったので、これを使用する。今回は平成17年の市町村別・死因別・性別・年齢階級別の死亡数を選んだ(→ソース)。平成17年にしたのは、国勢調査年なので後々便利かと思っただけで、深い理由はない。対応する人口データには、「住民基本台帳に基づく人口、人口動態及び世帯数調査」を用いた。市町村別・性別・年齢階級別の人口の年次データがe-statで手に入る(トップページから、「政府統計全体から探す」 >> 統計分野別「人口・世帯」 >> 「住民基本台帳に基づく人口、人口動態及び世帯数調査」 )。平成17年中の市町村合併を反映して、両データをマッチングする際には、夷隅町・大原町・岬町の3つをいすみ市に、干潟町・海上町・飯岡町の3つを旭市に計上した(→合併情報)。
【粗死亡率:人口規模を調整する】
死亡データを比較する時、死者数そのものを比べることにはほとんどの場合に意味がない。母数人口の規模が通常一定ではないからだ。言うまでもなく、人が多くいればそれだけ多くの死者が出やすいのだから、人口の差を加味しない比較はアンフェアである。
人口規模の違いを調整するために、死者数を母数人口で割ったものを「粗死亡率 (crude mortality rate, CMR)」と呼ぶ。小数点以下にゼロが並ぶと格好悪いので、10万をかけて「人口10万人あたり死亡者数」として計算するのが一般的。
CMR(i) = d(i) / n(i)
i: 地域
d(i): 地域iの死亡数
n(i): 地域iの人口
下図は、千葉県の各市町村について、心疾患(高血圧性を除く)による粗死亡率を求め、人口との散布図を描いたもの。強い負の相関が確認できる。なぜ負の相関なのか?
「人口規模が小さくなると心疾患のリスクが高まる」、と考えるのは早合点。これは典型的な擬似相関と見るべきだ。つまり、人口の小さいところは相対的に田舎で、高齢者の割合が大きく、そのため心疾患による死亡率が高くなるというわけだ。そういうわけで、千葉市と三芳村を比べるには、粗死亡率ではまだ不適格ということになる。人口規模の次は、人口構成の違いを調整する必要がある。
【つづき】
PR
AKB48得票数分析の最終回。
前々回の記事では、第3回選抜総選挙の得票数と順位の関係について、指数近似のフィットがかなり良いことを示し、前回の記事では得票数が順位の指数関数となるのは、得票数がlog-uniform分布に従う時であることを導いた。
今回はまとめとして、第1回から第3回までのデータを用いて、rank-frequency plot をもう一度よく見直し、議論を一旦締める。
データはこちら。ソースはここ。
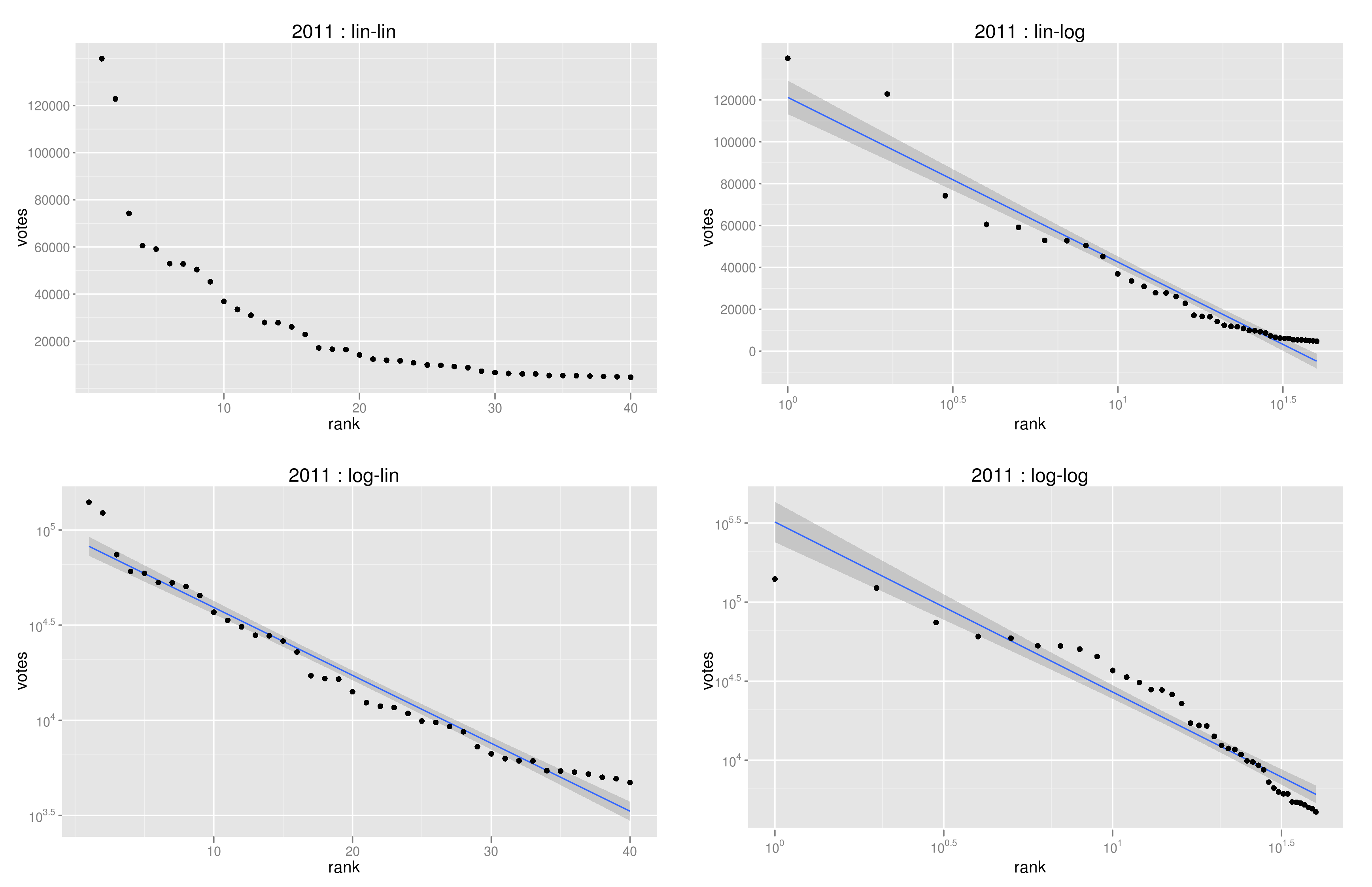
下図は、2011年のRank-frequency plotを4種類のスケールで描いたもの。lin-linは、両軸をそのままに、log-linはy軸を対数軸、lin-logはx軸を対数軸、log-logは両対数軸である。軸の取り方と得票数の分布の関係をまとめておくと
この図で比べてみると、やはりlog-lin(左下)の近似が一番良さそうに見える。
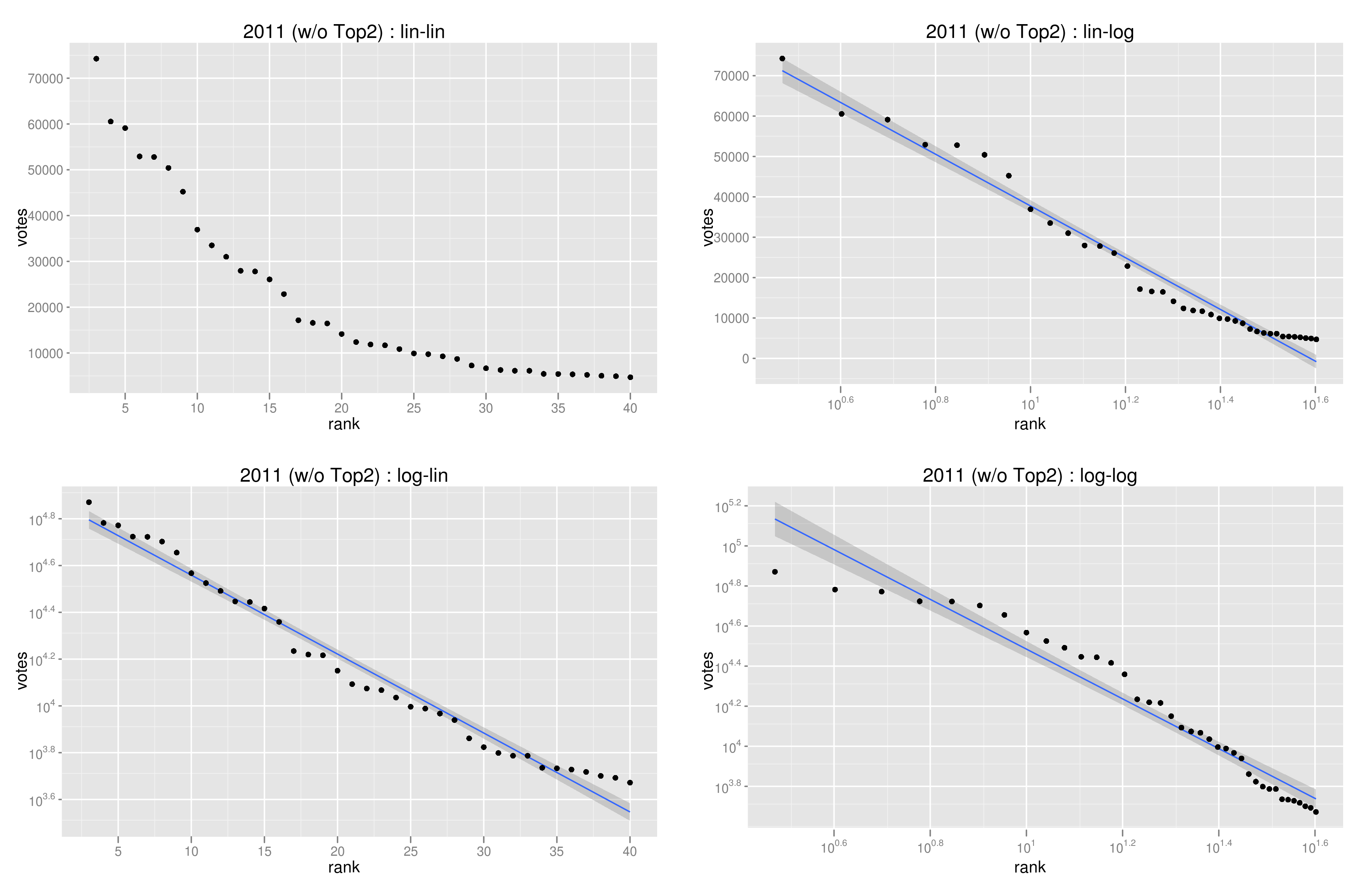
ただし、上位2名を除いて描き直してみると、結構難しいところ。これでも若干log-linが良さそうかな、と思う。
第1,2回ではさらに判断が難しい→2010年のグラフ, 2009年のグラフ。2010年ではlog-linとlin-logでともに綺麗な直線になっており、甲乙つけ難い。2009年では、むしろlog-logとlin-logがデッドヒートだ。総合すると、得票数の分布としてどれが一番有力であるかを視覚的に決めるのは難しい。統計的な検定をすることは理論的には可能だが、サンプルが30ないし40ではその力は限定的だろう。
実際のところ、1つの分布に限定する必要は必ずしもない。状況により、これらの分布の間を行ったり来たりするというのが答えかもしれない。たとえば、所得分布の研究では、高所得層ではパレート分布、中・低所得層では指数分布の当てはまりが良いことが知られている。ということは、何らかの要因でパレート分布に近くなったり指数分布に近くなったりする、というのもありそうな話だ。また、log-uniform分布とパレート分布は数学的には親戚関係にある。というのは、累積密度関数はそれぞれ
F(x) = a * log(x) + junk
F(x) = b * x^r + junk
であるので、これを微分して確率密度関数を求めると
f(x) ∝ x^(-1)
f(x) ∝ x^(r-1)
になる。つまり、パレート分布のパラメータ r をゼロに近づけていくと、だんだんとlog-uniform分布に近づいていくわけだ。
AKB48のことを調べて何になるかと言われれば全く何にもならないのだが、(AKBに限らず一般に)得票数の分布を真剣に分析した研究は少ないのではないかと思う。経済社会的な要因が政党の得票数にどう影響を与えるか、というのは政治経済学の王道トピックだが、得票数の分布に目を向けた話はあまり聞かない。もしかしたら、計量政治学の最も盛んな米国が二大政党制であるため、候補者数が2人の選挙が多くて分布も何もない、というのが原因かも(?)。他の国、例えば日本では政党数はそこそこあるし、小選挙区でも5人くらいの候補者がいる。知事選や地方議会選挙では数十人になることもある。するとそこには必然的に分布というものが発生するのである。
民主政治の根幹である「投票」について、分布から接近する手はないものか、とアイドルグループの人気投票を眺めながらそんなことを考えているのである。
【追記】
先行研究があった。1週間前の速報段階で全く同じことをやった人→YusukeMaedaさんのブログ。一年前の記事→ネット研。
前々回の記事では、第3回選抜総選挙の得票数と順位の関係について、指数近似のフィットがかなり良いことを示し、前回の記事では得票数が順位の指数関数となるのは、得票数がlog-uniform分布に従う時であることを導いた。
今回はまとめとして、第1回から第3回までのデータを用いて、rank-frequency plot をもう一度よく見直し、議論を一旦締める。
データはこちら。ソースはここ。
下図は、2011年のRank-frequency plotを4種類のスケールで描いたもの。lin-linは、両軸をそのままに、log-linはy軸を対数軸、lin-logはx軸を対数軸、log-logは両対数軸である。軸の取り方と得票数の分布の関係をまとめておくと
- lin-linで直線 ⇔ 一様分布
- log-linで直線 ⇔ log-uniform分布
- lin-logで直線 ⇔ 指数分布
- log-logで直線 ⇔ パレート分布
この図で比べてみると、やはりlog-lin(左下)の近似が一番良さそうに見える。
ただし、上位2名を除いて描き直してみると、結構難しいところ。これでも若干log-linが良さそうかな、と思う。
第1,2回ではさらに判断が難しい→2010年のグラフ, 2009年のグラフ。2010年ではlog-linとlin-logでともに綺麗な直線になっており、甲乙つけ難い。2009年では、むしろlog-logとlin-logがデッドヒートだ。総合すると、得票数の分布としてどれが一番有力であるかを視覚的に決めるのは難しい。統計的な検定をすることは理論的には可能だが、サンプルが30ないし40ではその力は限定的だろう。
実際のところ、1つの分布に限定する必要は必ずしもない。状況により、これらの分布の間を行ったり来たりするというのが答えかもしれない。たとえば、所得分布の研究では、高所得層ではパレート分布、中・低所得層では指数分布の当てはまりが良いことが知られている。ということは、何らかの要因でパレート分布に近くなったり指数分布に近くなったりする、というのもありそうな話だ。また、log-uniform分布とパレート分布は数学的には親戚関係にある。というのは、累積密度関数はそれぞれ
F(x) = a * log(x) + junk
F(x) = b * x^r + junk
であるので、これを微分して確率密度関数を求めると
f(x) ∝ x^(-1)
f(x) ∝ x^(r-1)
になる。つまり、パレート分布のパラメータ r をゼロに近づけていくと、だんだんとlog-uniform分布に近づいていくわけだ。
AKB48のことを調べて何になるかと言われれば全く何にもならないのだが、(AKBに限らず一般に)得票数の分布を真剣に分析した研究は少ないのではないかと思う。経済社会的な要因が政党の得票数にどう影響を与えるか、というのは政治経済学の王道トピックだが、得票数の分布に目を向けた話はあまり聞かない。もしかしたら、計量政治学の最も盛んな米国が二大政党制であるため、候補者数が2人の選挙が多くて分布も何もない、というのが原因かも(?)。他の国、例えば日本では政党数はそこそこあるし、小選挙区でも5人くらいの候補者がいる。知事選や地方議会選挙では数十人になることもある。するとそこには必然的に分布というものが発生するのである。
民主政治の根幹である「投票」について、分布から接近する手はないものか、とアイドルグループの人気投票を眺めながらそんなことを考えているのである。
【追記】
先行研究があった。1週間前の速報段階で全く同じことをやった人→YusukeMaedaさんのブログ。一年前の記事→ネット研。
前回の記事で、AKB48の総選挙得票数について、次のように結論づけた:
「第3回AKB48選抜総選挙の得票数は、順位の指数関数である」
実はこの文、当初は
「第3回AKB48選抜総選挙の得票数は、指数分布に従う」
となっていたのだが、ちょっと真偽が怪しいと思って書き直したのだ。
きちんと数式を解いたところ、やはりこの2つの文は同値ではないようだ。
前回の記事において、僕は、得票数と順位の関係を散布図に表し、それが指数関数でかなりよく近似できることを示した。この得票数と順位の散布図のことを rank-frequency plot という。この呼称は、この手の分析のパイオニアであるZiph先生が、シェイクスピア作品における単語の出現頻度(frequency)を分析したことに由来している(M.E.J. Newman, "Power laws, Pareto distributions and Zipf's law," Contemporary Physics 46(5), 2005 の Appendix Aを参照。→PDFへのリンク)。分析対象が変わっても rank-frequency plotと呼ぶのはややこしいことこの上ないのだが、とにかく、ここでfrequencyに該当するのは得票数であるということだ。
さて前回の結論を数式に表すと、
x = a * b^r .... (1)
x: 得票数, r: 順位
となる。簡単化のために、両辺に対数を取っておこう。
log(x) = C + D*r .... (1')
C=log(a), D=log(b)
今考えたいのは、「このようなrank-frequency plotを導くようなxの分布は何か」、ということだ。当初は考えもなしに「そりゃ指数分布だろ」と決め付けていたのだが、この第一感は怪しい。
x の累積密度関数をF(x)としよう。定義より、x よりも得票数の大きい人の割合は、1 - F(x) である。仮に母数をNとすれば、得票数 x の人の順位 r は、
r = [ 1 - F(x) ] * N .... (2)
と表せる。
したがって、(1'), (2)を用いてrを消去することにより
F(x) = α + β*log(x) .... (3)
α=1 + C/ND, β=-1/ND
を得る。
いくつか満たすべき条件がある。F(x)は0~1の値をとる単調増加関数なので、まずβ>0でなくてはいけない。また、xの値域は、 exp(-α/β) ≦ x ≦ exp((1-α)/β) である。
β>0の条件について考えておこう。定数の定義より、β>0 ⇔ D<0 ⇔ b∈(0,1) である。前回の記事でのbの値は0.9くらいだから、この条件を満たしている。
さて、(3) の分布はあまり見覚えのない式だが、どういう分布なのだろうか。y=log(x)と置くと見えやすいかもしれない(つまり yは得票数の自然対数)。するとy の累積密度関数 G は、
G(t) = Pr( y ≦ t ) = Pr( log(x) ≦ t ) = Pr( x ≦ exp(t) ) = F( exp(t) ) = α + β*t
と求められる。累積分布が一次関数、といえば答えは1つしかない:一様分布である。
結論: ある確率変数が log-uniform分布(対数を取ると一様分布)に従うならば、そのrank-frequency plot は指数関数になる。
百聞は一見に如かず。シミュレーションで確認してみよう(使用したRコード ggplot2パッケージが必要)。
下図は、[0,1]区間の一様分布に従う乱数を1000個発生させ、そのexponentialをxとして、rank-frequency plotを描いたもの(y軸のみ対数軸)。綺麗な直線を描いており、上の議論の裏が取れた。
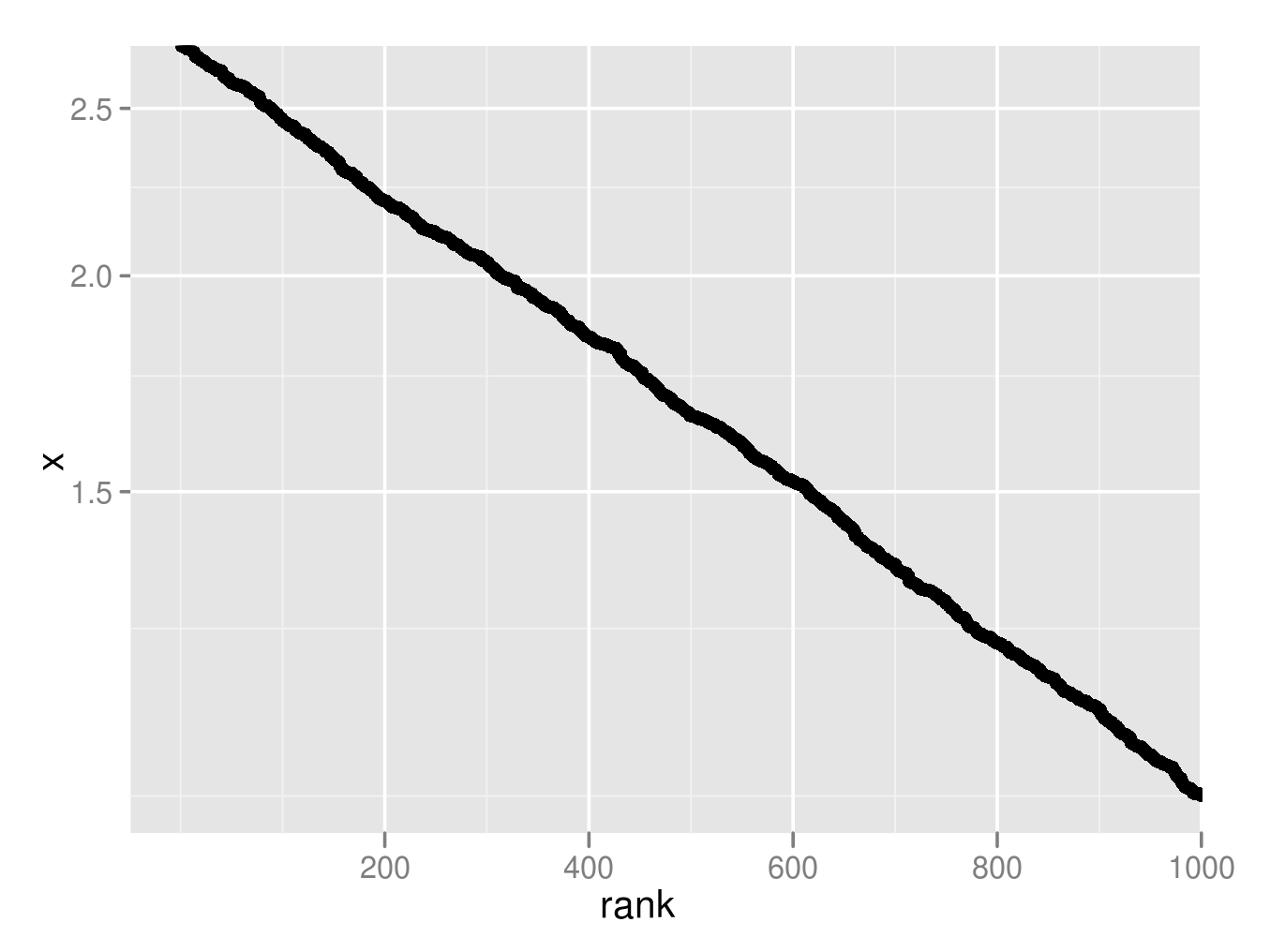
ちなみに、指数分布の rank-frequency plot はどうなるだろうか。どうも、対数を取るべき軸が逆転するようだ。というのも、計算すると分かるが、
x = a + b*log(r)
r: 順位
となるのである。
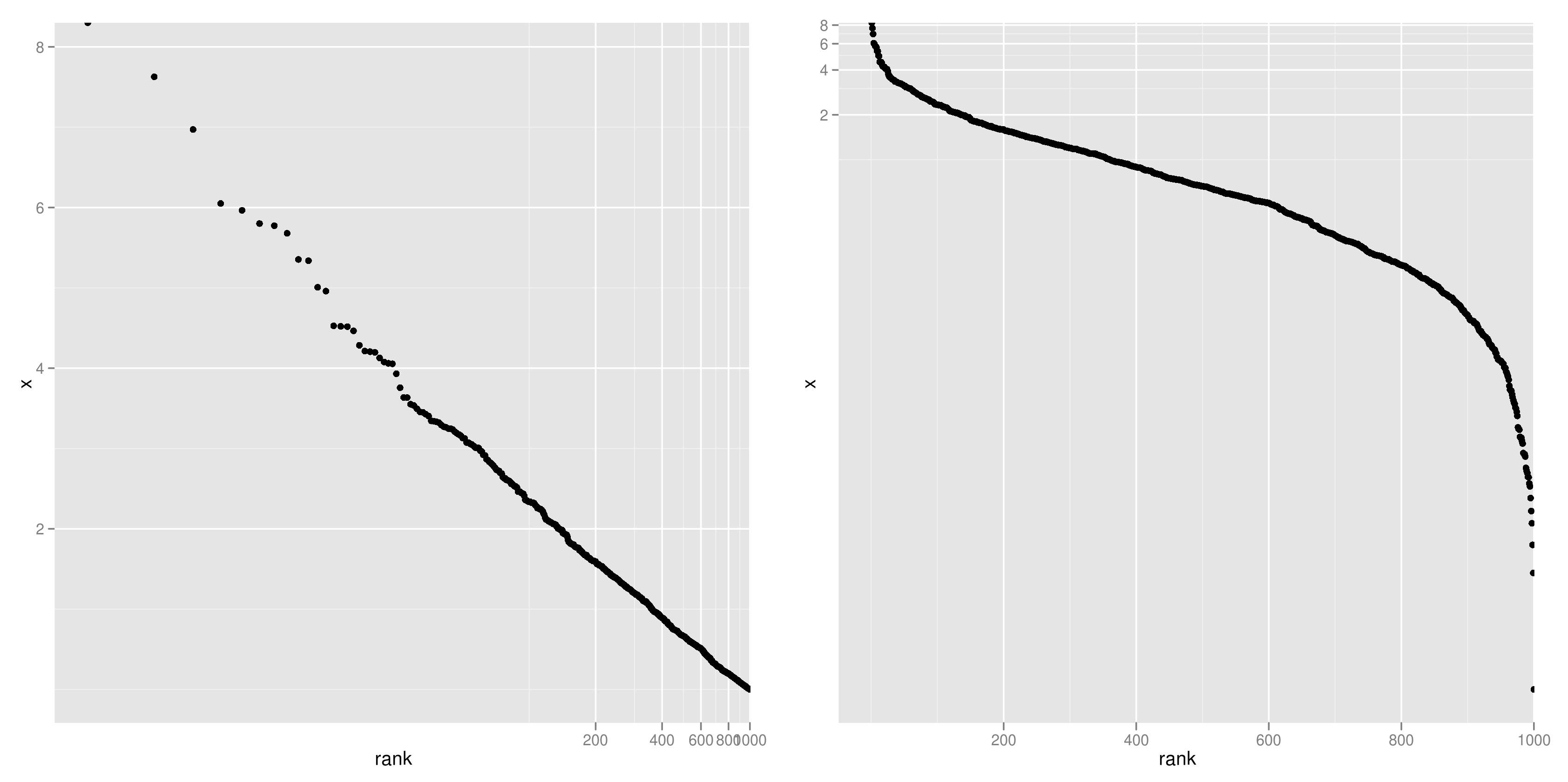
下図は、指数分布に従う乱数について rank-frequency plotを描いたものだが、順位にのみ対数を取る(左)と直線になることが分かる。一方、y軸のみを対数軸とする(右)とまるっきり直線にはならない。ゆえに、「第3回AKB48選抜総選挙の得票数は、指数分布に従う」は早とちりだったわけである。
というわけで、今回のAKB48の得票数分布については、log-uniformが有力候補である。なぜこの分布が現れるのか、という議論はかなり興味深いが、今のところビシッとした答えはでない。
【つづき】
「第3回AKB48選抜総選挙の得票数は、順位の指数関数である」
実はこの文、当初は
「第3回AKB48選抜総選挙の得票数は、指数分布に従う」
となっていたのだが、ちょっと真偽が怪しいと思って書き直したのだ。
きちんと数式を解いたところ、やはりこの2つの文は同値ではないようだ。
前回の記事において、僕は、得票数と順位の関係を散布図に表し、それが指数関数でかなりよく近似できることを示した。この得票数と順位の散布図のことを rank-frequency plot という。この呼称は、この手の分析のパイオニアであるZiph先生が、シェイクスピア作品における単語の出現頻度(frequency)を分析したことに由来している(M.E.J. Newman, "Power laws, Pareto distributions and Zipf's law," Contemporary Physics 46(5), 2005 の Appendix Aを参照。→PDFへのリンク)。分析対象が変わっても rank-frequency plotと呼ぶのはややこしいことこの上ないのだが、とにかく、ここでfrequencyに該当するのは得票数であるということだ。
さて前回の結論を数式に表すと、
x = a * b^r .... (1)
x: 得票数, r: 順位
となる。簡単化のために、両辺に対数を取っておこう。
log(x) = C + D*r .... (1')
C=log(a), D=log(b)
今考えたいのは、「このようなrank-frequency plotを導くようなxの分布は何か」、ということだ。当初は考えもなしに「そりゃ指数分布だろ」と決め付けていたのだが、この第一感は怪しい。
x の累積密度関数をF(x)としよう。定義より、x よりも得票数の大きい人の割合は、1 - F(x) である。仮に母数をNとすれば、得票数 x の人の順位 r は、
r = [ 1 - F(x) ] * N .... (2)
と表せる。
したがって、(1'), (2)を用いてrを消去することにより
F(x) = α + β*log(x) .... (3)
α=1 + C/ND, β=-1/ND
を得る。
いくつか満たすべき条件がある。F(x)は0~1の値をとる単調増加関数なので、まずβ>0でなくてはいけない。また、xの値域は、 exp(-α/β) ≦ x ≦ exp((1-α)/β) である。
β>0の条件について考えておこう。定数の定義より、β>0 ⇔ D<0 ⇔ b∈(0,1) である。前回の記事でのbの値は0.9くらいだから、この条件を満たしている。
さて、(3) の分布はあまり見覚えのない式だが、どういう分布なのだろうか。y=log(x)と置くと見えやすいかもしれない(つまり yは得票数の自然対数)。するとy の累積密度関数 G は、
G(t) = Pr( y ≦ t ) = Pr( log(x) ≦ t ) = Pr( x ≦ exp(t) ) = F( exp(t) ) = α + β*t
と求められる。累積分布が一次関数、といえば答えは1つしかない:一様分布である。
結論: ある確率変数が log-uniform分布(対数を取ると一様分布)に従うならば、そのrank-frequency plot は指数関数になる。
百聞は一見に如かず。シミュレーションで確認してみよう(使用したRコード ggplot2パッケージが必要)。
下図は、[0,1]区間の一様分布に従う乱数を1000個発生させ、そのexponentialをxとして、rank-frequency plotを描いたもの(y軸のみ対数軸)。綺麗な直線を描いており、上の議論の裏が取れた。
ちなみに、指数分布の rank-frequency plot はどうなるだろうか。どうも、対数を取るべき軸が逆転するようだ。というのも、計算すると分かるが、
x = a + b*log(r)
r: 順位
となるのである。
下図は、指数分布に従う乱数について rank-frequency plotを描いたものだが、順位にのみ対数を取る(左)と直線になることが分かる。一方、y軸のみを対数軸とする(右)とまるっきり直線にはならない。ゆえに、「第3回AKB48選抜総選挙の得票数は、指数分布に従う」は早とちりだったわけである。
というわけで、今回のAKB48の得票数分布については、log-uniformが有力候補である。なぜこの分布が現れるのか、という議論はかなり興味深いが、今のところビシッとした答えはでない。
【つづき】
何でもランキングが出るとすぐにグラフを描きたくなるのは、職業病のようなものだ。仕事柄、混沌たるデータの中に一筋の秩序を見つけることを常に要求されるのだが、順位データは規則性が比較的見つかりやすく、気持ちいいのが特徴だ。
今夜は、ついさっき発表された第3回AKB48選抜総選挙の結果を少し眺めてみよう。数値はこのページから取得した。データはこちら。
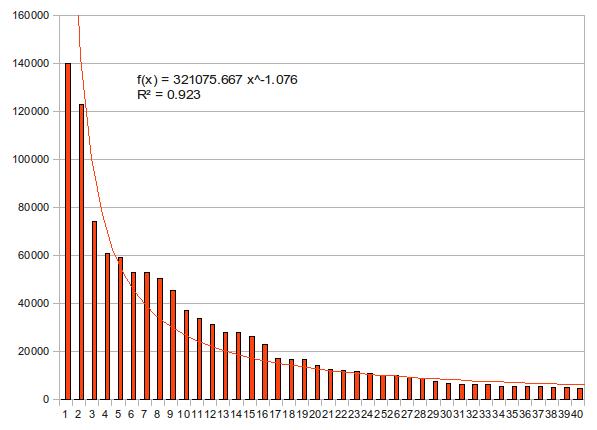
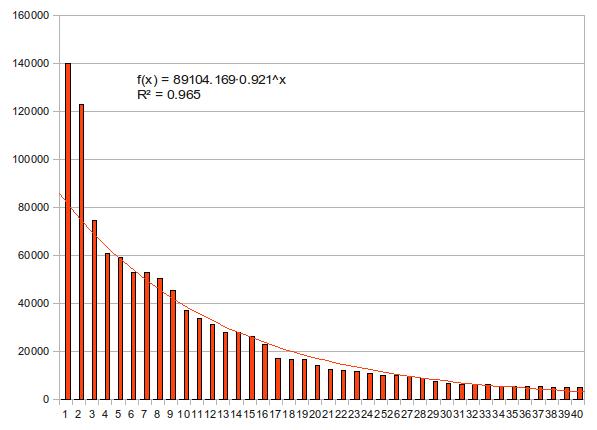
下の2つの図はどちらも上位40名の得票数を上から並べて棒グラフにしたものだが、近似曲線の描き方だけが異なっている。1つ目はべき関数、2つ目は指数関数で近似している。決定係数はどちらも0.9を越えて優秀だが、若干指数近似の方が値が高い。どちらの近似曲線がより「正しそう」か、もう少し見てみよう。
早稲田大学の西原先生は、微分方程式のゼミで、「人の目では直線くらいしか判断がつかない」と言っていた。曲線を見てそれがべき関数なのか指数関数なのかを判断するのは、人の知覚能力では困難だという教えだ(Yaleの同級生である戸田アレクシ哲が、あるグラフを見て「一目で双翼の指数分布だと気づいた」と言った時にはそのセンスに驚愕した)。非線形な関係にあるグラフを視覚的に判断するには、線形(ここではlinearではなくaffineの意)になるように上手いこと軸のスケールを変えるのが常用手段だ。
べき関数は、
y = a * x^r
という関係なので、両辺に対数を取ると
log(y) = C + r log(x)
C=log(a)
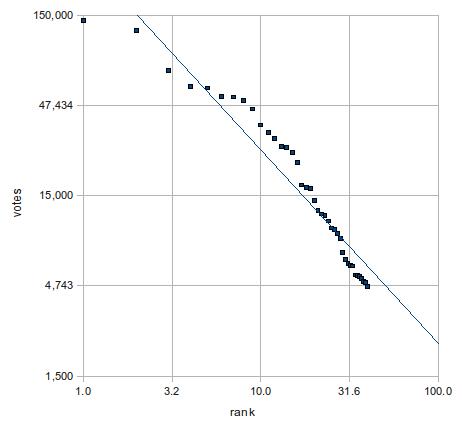
となる。そこで、x, yの両軸を対数にしたのが下図。
一方、指数近似では
y = a * b^x
という式に当てはめているので、
log(y) = C + D x
C =log(a), D=log(b)
つまり、片対数で直線になる。そこで下図ではy軸のみ対数にしてある。
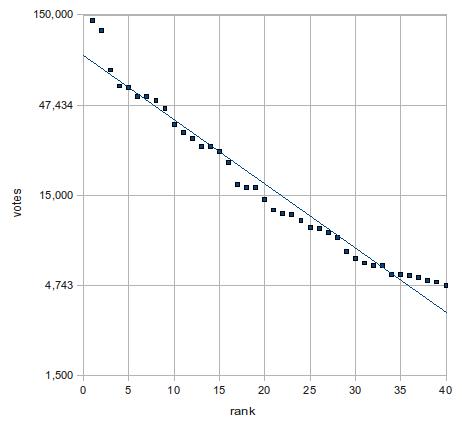
上の2つのグラフを比べれば、後者の近似がかなり有力であることは明らかだろう。ただし、上位2名(つまり、前田淳子と大島優子)は近似直線から大きくずれている。外れ値というやつだ。そこで、この2人を除いた3位から40位で改めて指数関数に当てはめてみよう。下図の通り、決定係数はさらに上がり、視覚的にもほぼ完璧に直線の上にデータが乗っている。
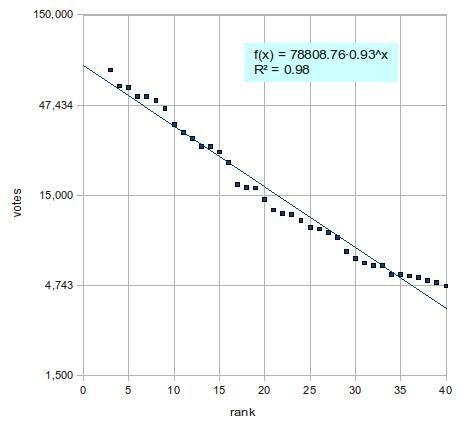
結論:第3回AKB48選抜総選挙の得票数は、順位の指数関数である。ただし、上位2人は外れ値。
上位2人だけが大きく外れる理由ははっきりとは分からないが、センターポジションに特別な意味があるということだろうか。
【つづき】
【追記】
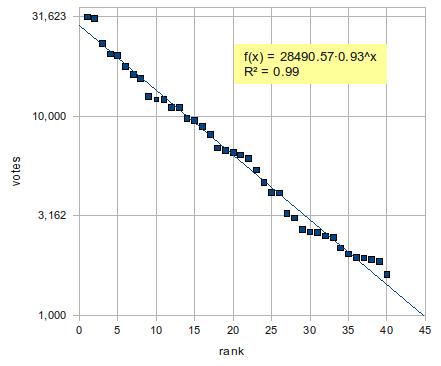
昨年のデータで同じことをやったところ、同様に指数関数の当てはまりが極めて良く、かつ上位2人はやや外れ値だった。2回連続でこれなら偶然ではなさそうだ。何か、こういう分布を生じさせるメカニズムが存在すると見て間違いない。データはこちら。
今夜は、ついさっき発表された第3回AKB48選抜総選挙の結果を少し眺めてみよう。数値はこのページから取得した。データはこちら。
下の2つの図はどちらも上位40名の得票数を上から並べて棒グラフにしたものだが、近似曲線の描き方だけが異なっている。1つ目はべき関数、2つ目は指数関数で近似している。決定係数はどちらも0.9を越えて優秀だが、若干指数近似の方が値が高い。どちらの近似曲線がより「正しそう」か、もう少し見てみよう。
早稲田大学の西原先生は、微分方程式のゼミで、「人の目では直線くらいしか判断がつかない」と言っていた。曲線を見てそれがべき関数なのか指数関数なのかを判断するのは、人の知覚能力では困難だという教えだ(Yaleの同級生である戸田アレクシ哲が、あるグラフを見て「一目で双翼の指数分布だと気づいた」と言った時にはそのセンスに驚愕した)。非線形な関係にあるグラフを視覚的に判断するには、線形(ここではlinearではなくaffineの意)になるように上手いこと軸のスケールを変えるのが常用手段だ。
べき関数は、
y = a * x^r
という関係なので、両辺に対数を取ると
log(y) = C + r log(x)
C=log(a)
となる。そこで、x, yの両軸を対数にしたのが下図。
一方、指数近似では
y = a * b^x
という式に当てはめているので、
log(y) = C + D x
C =log(a), D=log(b)
つまり、片対数で直線になる。そこで下図ではy軸のみ対数にしてある。
上の2つのグラフを比べれば、後者の近似がかなり有力であることは明らかだろう。ただし、上位2名(つまり、前田淳子と大島優子)は近似直線から大きくずれている。外れ値というやつだ。そこで、この2人を除いた3位から40位で改めて指数関数に当てはめてみよう。下図の通り、決定係数はさらに上がり、視覚的にもほぼ完璧に直線の上にデータが乗っている。
結論:第3回AKB48選抜総選挙の得票数は、順位の指数関数である。ただし、上位2人は外れ値。
上位2人だけが大きく外れる理由ははっきりとは分からないが、センターポジションに特別な意味があるということだろうか。
【つづき】
【追記】
昨年のデータで同じことをやったところ、同様に指数関数の当てはまりが極めて良く、かつ上位2人はやや外れ値だった。2回連続でこれなら偶然ではなさそうだ。何か、こういう分布を生じさせるメカニズムが存在すると見て間違いない。データはこちら。
先月11日に授業用の論文を8月2日までに書き直して再提出せよというemailを教官から受け取り狼狽しました。というのも彼の口ぶりが、もともと再提出しなければ単位要件を満たさないって言ってあっただろうという様子だったからです。こちらとしてはもう単位をもらった気でいたので、嫌な汗をぶわっとかきました。
確かに1度目の提出後に受け取ったコメントを眺めてみると、「~を改善すれば講義の要求するレベルを満足するだろう」と書いてありました。ですが、ここから「したがって書き直して再提出せよ」というメッセージを察知できなかったのです。もしこれを察知していたならW杯の合間を縫ってちゃくちゃくと筆を進めていただろうに、またもや突貫工事をする羽目になりました。
そういうわけで先週書き直して提出しました。こういう課題は気が滅入るものです。ちゃんと物事をこなしている人たちはとっくに済ませているのだと思うと自己嫌悪になりますし、たとえこの課題を終わらせても他人に先んじることにはならないのだと思うとモチベーションも上がってきません。兎にも角にも、先週終わらせたのです。
今日その先生から届いたemailを読んでみますと「8月2日が締切りであることを再度伝える(すでに6人の生徒は提出済みである)」とあります。どうやら再提出が延び延びになっていたのは僕の他にも沢山いるようです。ここまでくると、もはやこれは教授の不備であると言わざるを得ません。
確かに1度目の提出後に受け取ったコメントを眺めてみると、「~を改善すれば講義の要求するレベルを満足するだろう」と書いてありました。ですが、ここから「したがって書き直して再提出せよ」というメッセージを察知できなかったのです。もしこれを察知していたならW杯の合間を縫ってちゃくちゃくと筆を進めていただろうに、またもや突貫工事をする羽目になりました。
そういうわけで先週書き直して提出しました。こういう課題は気が滅入るものです。ちゃんと物事をこなしている人たちはとっくに済ませているのだと思うと自己嫌悪になりますし、たとえこの課題を終わらせても他人に先んじることにはならないのだと思うとモチベーションも上がってきません。兎にも角にも、先週終わらせたのです。
今日その先生から届いたemailを読んでみますと「8月2日が締切りであることを再度伝える(すでに6人の生徒は提出済みである)」とあります。どうやら再提出が延び延びになっていたのは僕の他にも沢山いるようです。ここまでくると、もはやこれは教授の不備であると言わざるを得ません。
Calender
| 12 | 2026/01 | 02 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Search in This Blog
Latest Comments
[03/30 川内のばば山田]
[03/30 川内のばば山田]
[08/06 Aterarie]
[07/05 Agazoger]
[07/01 Thomaskina]
Latest Posts
(11/16)
(04/28)
(04/16)
(04/11)
(04/05)
Latest Trackbacks
Category
Access Analysis

