Yaleで、遊んで学ぶ日々。
Yaleで、遊んで学ぶ日々。
囲碁、ときどきプログラミング、ところにより経済。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
RとC言語の連携の仕方を最近知った。友人の情報によると、サンタフェの人たちが言うには、この連携機能こそがMatlabにはない魅力なのだそうだ。
普通の回帰分析をやっている分には別にCなんて触れない方がいい。デバッグが面倒くさいだけだ。しかし、ちょっと面倒なことをやりたい時には、もしかしたらCと連携することで劇的な速度改善が見込めるかもしれない。
連携の良いところは、乗り換えではないということだ。原則としてRで作業して、計算が大変なところだけCの力を借りれば良い。例えば、データを読み込んで整形するところまでをRでやって、最尤法でパラメータを推計するために、最適化問題を解く所だけCのメソッドを利用する、という感じだろうか。やったことがないから想像の域をでないが、1日色々実験したところ、できそうな気がする。
今日は、Rをはじめとするインタープリタ言語が苦手であると言われているループ処理において、どれくらい差が出るのか試してみた。
作業内容はこちら↓↓
N <- 100
out <- 0
N * N の行列を、左上から右へ進み、各セルにおいてそのセルの行番号を足し、列番号を引く。右端に行き着いたら次の行へ・・・。対象なので答えは必ずゼロになるからプログラムとしてはまったく無意味なのだが、ポイントはN^2回の計算をするためNが増えると計算量が急激にあがるということだ。
結果は以下の通り。tC, tRはそれぞれCのメソッドを利用した場合, 通常どおりRでやった場合にかかった時間だ。差は歴然。正直ここまで違うとは思ってなかった。
N tC tR
グラフにするとこんな感じ。
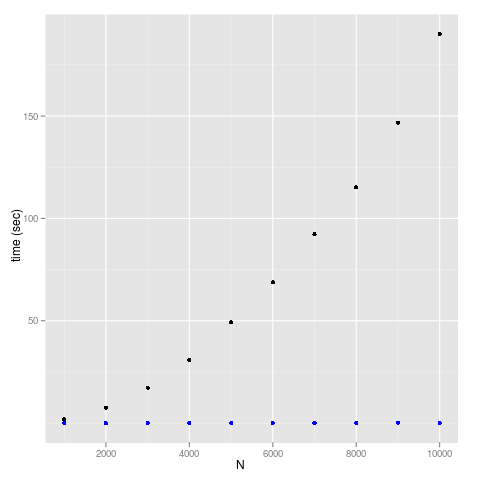
これじゃぱっと見よく分からないから、両対数にしてみる。すると、面白いことにほぼ平行な直線の上に乗っているようだ。
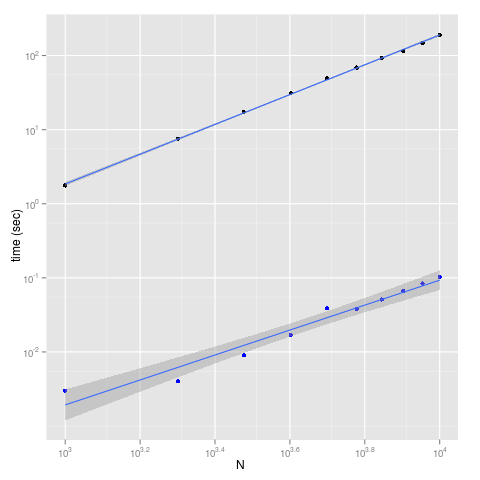
最小二乗法で推計してみると、
log(tC) = -17.88 + 1.68 log(N)
log(tR) = -13.28 + 2.01 log(N)
という結果。tRの方は、2重ループの場合、理論的にlog(N)の係数は2になるんだろう。tCの方は、標準誤差が0.13なのでlog(N)の係数が2であるという仮説は、一般的な有意水準で棄却される。Cのメソッドを使った方がサイズに対する弾力性がほんの少し低い(のかな?)。むしろ、大きな差の源泉は切片の方にあるようだ。
普通の回帰分析をやっている分には別にCなんて触れない方がいい。デバッグが面倒くさいだけだ。しかし、ちょっと面倒なことをやりたい時には、もしかしたらCと連携することで劇的な速度改善が見込めるかもしれない。
連携の良いところは、乗り換えではないということだ。原則としてRで作業して、計算が大変なところだけCの力を借りれば良い。例えば、データを読み込んで整形するところまでをRでやって、最尤法でパラメータを推計するために、最適化問題を解く所だけCのメソッドを利用する、という感じだろうか。やったことがないから想像の域をでないが、1日色々実験したところ、できそうな気がする。
今日は、Rをはじめとするインタープリタ言語が苦手であると言われているループ処理において、どれくらい差が出るのか試してみた。
作業内容はこちら↓↓
N <- 100
out <- 0
for (i in 1:N) {
for (j in 1:N) {
out <- out + i - j
}
}
N * N の行列を、左上から右へ進み、各セルにおいてそのセルの行番号を足し、列番号を引く。右端に行き着いたら次の行へ・・・。対象なので答えは必ずゼロになるからプログラムとしてはまったく無意味なのだが、ポイントはN^2回の計算をするためNが増えると計算量が急激にあがるということだ。
結果は以下の通り。tC, tRはそれぞれCのメソッドを利用した場合, 通常どおりRでやった場合にかかった時間だ。差は歴然。正直ここまで違うとは思ってなかった。
N tC tR
1000 0.003 1.766
2000 0.004 7.513
3000 0.009 17.313
4000 0.017 30.836
5000 0.039 49.249
6000 0.038 68.721
7000 0.051 92.286
8000 0.066 115.140
9000 0.084 146.736
10000 0.102 190.155
グラフにするとこんな感じ。
これじゃぱっと見よく分からないから、両対数にしてみる。すると、面白いことにほぼ平行な直線の上に乗っているようだ。
最小二乗法で推計してみると、
log(tC) = -17.88 + 1.68 log(N)
log(tR) = -13.28 + 2.01 log(N)
という結果。tRの方は、2重ループの場合、理論的にlog(N)の係数は2になるんだろう。tCの方は、標準誤差が0.13なのでlog(N)の係数が2であるという仮説は、一般的な有意水準で棄却される。Cのメソッドを使った方がサイズに対する弾力性がほんの少し低い(のかな?)。むしろ、大きな差の源泉は切片の方にあるようだ。
PR
| R: コンソールでやるのもそこまで悪くない << | HOME | >> 最初に言え |
Calender
| 10 | 2025/11 | 12 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
Search in This Blog
Latest Comments
[03/30 川内のばば山田]
[03/30 川内のばば山田]
[08/06 Aterarie]
[07/05 Agazoger]
[07/01 Thomaskina]
Latest Posts
(11/16)
(04/28)
(04/16)
(04/11)
(04/05)
Latest Trackbacks
Category
Access Analysis

